
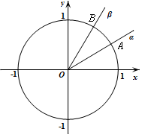
【题目】如图,在平面直角坐标系中,锐角![]() 、
、![]() 的终边分别与单位圆交于
的终边分别与单位圆交于![]() ,
,![]() 两点.
两点.
(1)如果![]() ,
,![]() 点的横坐标为
点的横坐标为![]() ,求
,求![]() 的值;
的值;
(2)若角![]() 的终边与单位圆交于C点,设角
的终边与单位圆交于C点,设角![]() 、
、![]() 、
、![]() 的正弦线分别为
的正弦线分别为![]() ,求证:线段
,求证:线段![]() 能构成一个三角形;
能构成一个三角形;
(3)探究第(2)小题中的三角形的外接圆面积是否为定值?若是,求出该定值;若不是,请说明理由.
【答案】(1)![]() ;(2)证明详见解析;(3)
;(2)证明详见解析;(3)![]() .
.
【解析】
试题分析:(1)由同角间基本关系式,由![]() 可得
可得![]() ,
,![]() 据三角函数定义可得
据三角函数定义可得![]() ,
,![]() ,由两角和的余弦公式将
,由两角和的余弦公式将![]() 展开代入可得其值;(2)由题意知
展开代入可得其值;(2)由题意知![]() ,
,![]() ,
,![]() .再利用正余弦值证明两边之和大于第三边和二边之差小于第三边,可判断三条线段能构成一个三角形;(3) 设
.再利用正余弦值证明两边之和大于第三边和二边之差小于第三边,可判断三条线段能构成一个三角形;(3) 设![]() 的边长分别为
的边长分别为![]() ,由余弦定理可得
,由余弦定理可得![]() ,进一步得
,进一步得![]() ,再由正弦定理
,再由正弦定理![]() ,可得
,可得![]() 值.
值.
试题解析:
(1)已知![]() 是锐角,根据三角函数的定义,得
是锐角,根据三角函数的定义,得![]()
![]()
又![]() ,且
,且![]() 是锐角,所以
是锐角,所以![]() .
.
所以![]() .
.
(2)证明:依题意得,![]() ,
,![]() ,
,![]()
因为![]() ,所以
,所以![]() ,
,![]() ,于是有
,于是有
![]() ,①
,①
又∵![]() ,
,
![]() ,②
,②
同理,![]() ,③
,③
由①,②,③可得,线段![]() 能构成一个三角形.
能构成一个三角形.
(3)第(2)小题中的三角形的外接圆面积是定值,且定值为![]() .
.
不妨设![]() 的边长分别为
的边长分别为![]() ,其中角
,其中角![]() 、
、![]() 、
、![]() 的对边分别为
的对边分别为![]() .则由余弦定理,得:
.则由余弦定理,得:![]() .
.
![]()
![]()
![]()
![]()
因为![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
设![]() 的外接圆半径为R,由正弦定理,得
的外接圆半径为R,由正弦定理,得![]() ,∴
,∴![]() ,
,
所以![]() 的外接圆的面积为
的外接圆的面积为![]() .
.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中数学 来源: 题型:
【题目】某商品的价格前两年每年递增20%,后两年每年递减20%,最后一年的价格与原来的价格比较,变化情况是( )
(A)不增不减 (B)约增1.4%
(C)约减9.2% (D)约减7.8%
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知全集U=R,且A={x||x-1|>2},B={x|x2-6x+8<0},则(UA)∩B等于( )
A. [-1,4) B. (2,3)
C. (2,3] D. (-1,4)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某产品生产线上,一天内每隔60分钟抽取一件产品,则该抽样方法为①;某中学从30名机器人爱好者中抽取3人了解学习负担情况,则该抽取方法为②,那么
A. ①是系统抽样,②是简单随机抽样 B. ①是分层抽样,②是简单随机抽样
C. ①是系统抽样,②是分层抽样 D. ①是分层抽样,②是系统抽样
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题正确的是( )
A. 有两个面平行,其余各面都是四边形的几何体叫棱柱
B. 有两个面平行,其余各面都是平行四边形的几何体叫棱柱
C. 用一个平面去截棱锥,底面与截面之间的部分组成的几何体叫棱台
D. 有两个面平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行的几何体叫棱柱
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班数学课代表给全班同学出了一道证明题,以下四人中只有一人说了真话,只有一人会证明此题。甲:我不会证明。乙:丙会证明。丙:丁会证明。丁:我不会证明。根据以上条件,可以判定会证明此题的人是( )
A. 甲 B. 乙 C. 丙 D. 丁
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中正确的是( )
A. 棱柱的侧面可以是三角形
B. 正方体和长方体都是特殊的四棱柱
C. 所有的几何体的表面都能展成平面图形
D. 棱柱的各条棱都相等
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com