练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图所示，在ABCD中，∠BCD=90°，BC=CD=1，AC⊥平面BCD，∠ADC=45°，E是线段AD的中点，F是线段AC上的一个动点．

    (1)确定点F的位置，使平面ABD⊥平面BEF；

    (2)当平面ABD⊥平面BEF时，求直线DB与EF所成的角．

    解：(1)由已知可得AB=AD=BD=，又AE=ED，则BE⊥A D．

    由平面ABD⊥平面BEF得AD⊥平面BEF，故AD⊥EF，

    即F应为过点E的AD的垂线和AC的交点，由AC=CD知F点即为C点．

    (2)由(1)知，EF与BD所成的角即为EC与BD所成的角．

    延长AC至G，使得CG=AC，连接DG，

    则∠BDG即为CE与BD所成的角．

    在△BDG中，BD=DG=BG，所以∠BDG=60°，

    即直线EF与直线BD所成的角为60°．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：重难点手册　高中数学·必修4（配人教A版新课标） 人教A版新课标 题型：022

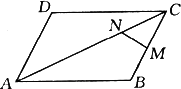
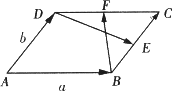
    如图所示，在□ABCD中，＝a，＝b，＝3，M为BC的中点，则＝________．(用a、b表示)

    查看答案和解析>>

    科目：高中数学 来源：“伴你学”新课程　数学·必修3、4(人教B版) 人教B版 题型：022

    如图所示，在□ABCD中，E，F分别为BC，DC的中点，若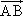＝a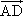，＝b，则以a，b为基底表示向量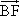为________，为________．

    查看答案和解析>>

    科目：高中数学 来源：选修设计数学A4－1人教版 人教版 题型：013

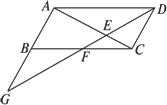
    如图所示，在□ABCD中，F是BC边上的点，延长DF与AB的延长线相交于G，则相似三角形有

    [　　]
    A．

    3对

    B．

    4对

    C．

    5对

    D．

    6对

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图所示，在ABCD中，已知=a，=b.

    （1）试用a、b表示、；

    （2）若|a+b|=|a-b|,试证：ABCD为矩形.

    查看答案和解析>>

    同步练习册答案