
【题目】函数![]() 的定义域为( )
的定义域为( )
A.![]()
B.![]()
C.![]()
D.![]()
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:
【题目】下列说法中,正确的是
·(1)任取x>0,均有3x>2x;
·(2)当a>0,且a≠1时,有a3>a2;
·(3)y=( ![]() )﹣x是减函数;
)﹣x是减函数;
·(4)函数f(x)在x>0时是增函数,x<0也是增函数,所以f(x)是增函数;
·(5)若函数f(x)=ax2+bx+2与x轴没有交点,则b2﹣8a<0且a>0;
·(6)y=x2﹣2|x|﹣3的递增区间为[1,+∞).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若二次函数f(x)=ax2+bx+c(a,b,c∈R)满足f(x+1)﹣f(x)=4x+1,且f(0)=3.
(1)求f(x)的解析式;
(2)若在区间[﹣1,1]上,不等式f(x)>6x+m恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a∈R,函数f(x)=x|x﹣a|.
(1)当a=2时,将函数f(x)写成分段函数的形式,并作出函数的简图,写出函数y=f(x)的单调递增区间;
(2)当a>2时,求函数y=f(x)在区间[1,2]上的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在锐角△ABC中,内角A,B,C的对边分别为a,b,c,且2asinB= ![]() b.
b.
(1)求角A的大小;
(2)若a=4,b+c=8,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(x﹣1)2+a(lnx﹣x+1)(其中a∈R,且a为常数) (Ⅰ)当a=4时,求函数y=f(x)的单调区间;
(Ⅱ)若对于任意的x∈(1,+∞),都有f(x)>0成立,求a的取值范围;
(Ⅲ)若方程f(x)+a+1=0在x∈(1,2)上有且只有一个实根,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题P:4x﹣a2x+1≥0对x∈[﹣1,1]恒成立,命题Q:f(x)=log2(ax2﹣2x+ ![]() )的值域是R,若满足P且Q为假,P或Q为真,求实数a的取值范围.
)的值域是R,若满足P且Q为假,P或Q为真,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,⊙O交直线OB于E、D,连接EC、CD. 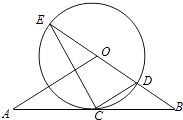
(1)求证:直线AB是⊙O的切线;
(2)若tan∠CED= ![]() ,⊙O的半径为3,求OA的长.
,⊙O的半径为3,求OA的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com