
| A. | $\frac{3}{7}$ | B. | -$\frac{3}{7}$ | C. | -$\frac{7}{3}$ | D. | $\frac{7}{3}$ |
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12 | B. | 20 | C. | 16 | D. | 32 |
查看答案和解析>>
科目:高中数学 来源:2017届广东佛山一中高三上学期月考一数学(理)试卷(解析版) 题型:选择题
已知全集U = R,集合 ,
, R│
R│ ≥
≥ ,下图中阴影部分所表示的集合为
,下图中阴影部分所表示的集合为

A. B.
B.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北冀州市高二文上月考三数学试卷(解析版) 题型:解答题
从一条生产线上每隔30分钟取一件产品,共取了 件,测得其产品尺寸后,画出其频率分布直方图如图,已知尺寸在
件,测得其产品尺寸后,画出其频率分布直方图如图,已知尺寸在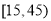 内的频数为92.
内的频数为92.

(Ⅰ)求 的值;
的值;
(Ⅱ)求尺寸在 内产品的个数;
内产品的个数;
(Ⅲ)估计尺寸大于25的频率.
查看答案和解析>>
科目:高中数学 来源:2016-2017学年广西陆川县中学高二理9月月考数学试卷(解析版) 题型:选择题
方程 表示的曲线为( )
表示的曲线为( )
A.一条线段与一段劣弧 B.一条射线与一段劣弧
C.一条射线与半圆 D.一条直线和一个圆
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com