
【题目】甲、乙两人做定点投篮游戏,已知甲每次投篮命中的概率均为![]() ,甲投篮3次均未命中的概率为
,甲投篮3次均未命中的概率为![]() ,乙每次投篮命中的概率均为
,乙每次投篮命中的概率均为![]() ,乙投篮2次恰好命中1次的概率为
,乙投篮2次恰好命中1次的概率为![]() ,甲、乙每次投篮是否命中相互之间没有影响.
,甲、乙每次投篮是否命中相互之间没有影响.
(1)若乙投篮3次,求至少命中2次的概率;
(2)若甲、乙各投篮2次,设两人命中的总次数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:
【题目】太原五中是一所有着百年历史的名校,图1是某一阶段来我校参观学习的外校人数统计茎叶图,第1次到第14次参观学习人数依次记为A1 , A2 , …,A14 , 图2是统计茎叶图中人数在一定范围内的一个算法流程图,那么算法流程图输出的结果是 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,且
,且![]() 在
在![]() 和
和![]() 处取得极值.
处取得极值.
(Ⅰ)求函数![]() 的解析式;
的解析式;
(Ⅱ)设函数![]() ,是否存在实数
,是否存在实数![]() ,使得曲线
,使得曲线![]() 与
与![]() 轴有两个交点,若存在,求出
轴有两个交点,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】心理学家发现视觉和空间能力与性别有关,孝感市黄陂路高中数学兴趣小组为了验证这个结论,从兴趣小组中抽取50名同学(男30女20),给所有同学几何题和代数题各一题,让各位同学自由选择一道题进行解答.选题情况如下表:(单位:人)

(1)能否据此判断有![]() 的把握认为视觉和空间能力与性别有关?
的把握认为视觉和空间能力与性别有关?
(2)以上列联表中女生选做几何题的频率作为概率,从该校1500名女生中随机选6名女生,记6名女生选做几何题的人数为![]() ,求
,求![]() 的数学期望
的数学期望![]() 和方差
和方差![]() .
.
附表:

参考公式: 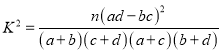 ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在半径为R的圆桌上摆放同样大小的半径为r的硬币.要求硬币不准露出圆桌面边缘,并且所摆硬币彼此不能重叠.当摆放n枚硬币之后,圆桌上就不能再多摆放一枚这种硬币了.求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】水葫芦原产于巴西,![]() 年作为观赏植物引入中国. 现在南方一些水域水葫芦已泛滥成灾严重影响航道安全和水生动物生长. 某科研团队在某水域放入一定量水葫芦进行研究,发现其蔓延速度越来越快,经过
年作为观赏植物引入中国. 现在南方一些水域水葫芦已泛滥成灾严重影响航道安全和水生动物生长. 某科研团队在某水域放入一定量水葫芦进行研究,发现其蔓延速度越来越快,经过![]() 个月其覆盖面积为
个月其覆盖面积为![]() ,经过
,经过![]() 个月其覆盖面积为
个月其覆盖面积为![]() . 现水葫芦覆盖面积
. 现水葫芦覆盖面积![]() (单位
(单位![]() )与经过时间
)与经过时间![]() 个月的关系有两个函数模型
个月的关系有两个函数模型![]() 与
与![]() 可供选择.
可供选择.
(参考数据:![]() )
)
(Ⅰ)试判断哪个函数模型更合适,并求出该模型的解析式;
(Ⅱ)求原先投放的水葫芦的面积并求约经过几个月该水域中水葫芦面积是当初投放的![]() 倍.
倍.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“双曲线的方程为![]() ”是“双曲线的渐近线方程为
”是“双曲线的渐近线方程为![]() ”的( )
”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
【答案】A
【解析】双曲线的方程为![]() ,则渐近线方程为
,则渐近线方程为![]() ,渐近线方程为:
,渐近线方程为: ![]() ,反之当渐近线方程为
,反之当渐近线方程为![]() 时,只需要满足
时,只需要满足![]() ,等轴双曲线即可.故选择充分不必要条件.
,等轴双曲线即可.故选择充分不必要条件.
故答案为:A.
【题型】单选题
【结束】
10
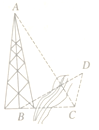
【题目】如图,为测量河对岸塔![]() 的高,先在河岸上选一点
的高,先在河岸上选一点![]() ,使
,使![]() 在塔底
在塔底![]() 的正东方向上,在点
的正东方向上,在点![]() 处测得
处测得![]() 点的仰角为
点的仰角为![]() ,再由点
,再由点![]() 沿北偏东
沿北偏东![]() 方向走
方向走![]() 到位置
到位置![]() ,测得
,测得![]() ,则塔
,则塔![]() 的高是( )
的高是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com