
 后与汽车相遇………………………………1分.
后与汽车相遇………………………………1分. ,则cosα=
,则cosα= .……………………4分
.……………………4分 .
. -80)2+3 600.……………………7分
-80)2+3 600.……………………7分 =
= ,即t=
,即t= 时,vmin2="3" 600.
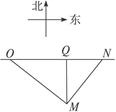
时,vmin2="3" 600. =15×25,MQ=300.
=15×25,MQ=300. 设∠MNO=β,则sinβ=
设∠MNO=β,则sinβ= =
= .
. 分
分

 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案科目:高中数学 来源:不详 题型:解答题
 站C,并在车站C也停留10分钟.已知早上8点时甲车从车站A、乙车从车站B同时开出.
站C,并在车站C也停留10分钟.已知早上8点时甲车从车站A、乙车从车站B同时开出. 离,及B,C两站距离;(2)若甲、乙两车上各有一名旅客需要交换到对方汽车上,问能否在车站C处利用停留时间交换.(3)求10点时甲、乙两车的距离.(可能用到的参考数据:
离,及B,C两站距离;(2)若甲、乙两车上各有一名旅客需要交换到对方汽车上,问能否在车站C处利用停留时间交换.(3)求10点时甲、乙两车的距离.(可能用到的参考数据: ,
, ,
, ,
, )
)
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,求
,求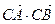 的最大值
的最大值查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com