
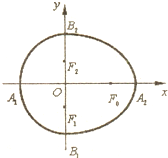
 请阅读以下材料,然后解决问题:
请阅读以下材料,然后解决问题:| y2 |
| b2 |
| x2 |
| c2 |
| x2 |
| a2 |
| y2 |
| b2 |
| ||||
| 4 |
| ||||
| 4 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
 根据题意,得
根据题意,得| y2 |
| b2 |
| x2 |
| c2 |
| 1 |
| 2 |
| b2-c2 |
| 1 |
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
| a2-b2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 4 |
| 1 |
| 2 |
| ||
| 4 |
| ||||
| 4 |
| ||||
| 4 |


科目:高中数学 来源:2008-2009学年广东省佛山一中高二(上)期末数学试卷(理科)(解析版) 题型:填空题
 +
+ =1 (x≤0)与半椭圆C2:
=1 (x≤0)与半椭圆C2: +
+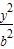 =1 (x≥0)合成的曲线称作“果圆”,其中a2=b2+c2,a>0,b>c>0
=1 (x≥0)合成的曲线称作“果圆”,其中a2=b2+c2,a>0,b>c>0
查看答案和解析>>
科目:高中数学 来源:广东省汕头金山中学09-10学年高二下学期期中考试(理) 题型:填空题
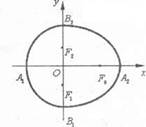 请阅读以下材料,然后解决问题:
请阅读以下材料,然后解决问题:
①设椭圆的长半轴长为a,短半轴长为b,则椭圆的面积为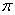 ab
ab
②我们把由半椭圆C1: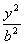 +
+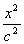 =1 (x≤0)与半椭圆C2:
=1 (x≤0)与半椭圆C2: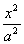 +
+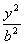 =1 (x≥0)合成的曲线称作“果圆”,其中
=1 (x≥0)合成的曲线称作“果圆”,其中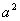 =
=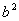 +
+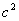 ,a>0,b>c>0
,a>0,b>c>0
如右上图,设点F0,F1,F2是相应椭圆的焦点,A1,A2和B1,B2是“果圆”与x,y轴的交点,若△F0 F1 F2是边长为1的等边三角形,则上述“果圆”的面积为 。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com