
【题目】在△ABC中,角A,B,C对应的边分别是a,b,c,已知cos 2A-3cos(B+C)=1.
(1)求角A的大小;
(2)若△ABC的面积S=5![]() ,b=5,求sin Bsin C的值.
,b=5,求sin Bsin C的值.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)根据二倍角公式![]() ,三角形内角和
,三角形内角和![]() ,所以
,所以![]() ,整理为关于
,整理为关于![]() 的二次方程,解得角
的二次方程,解得角![]() 的大小;(2)根据三角形的面积公式和上一问角
的大小;(2)根据三角形的面积公式和上一问角![]() ,代入后解得边
,代入后解得边![]() ,这样就知道
,这样就知道![]() ,然后根据余弦定理再求
,然后根据余弦定理再求![]() ,最后根据证得定理分别求得
,最后根据证得定理分别求得![]() 和
和![]() .
.
试题解析:(1)由cos 2A-3cos(B+C)=1,
得2cos2A+3cos A-2=0,
即(2cos A-1)(cos A+2)=0,
解得cos A=![]() 或cos A=-2(舍去).
或cos A=-2(舍去).
因为0<A<π,所以A=![]() .
.
(2)由S=![]() bcsin A=
bcsin A=![]() bc×
bc×![]() =
=![]() bc=5
bc=5![]() ,得bc=20,又b=5,知c=4.
,得bc=20,又b=5,知c=4.
由余弦定理得a2=b2+c2-2bccos A=25+16-20=21,故a=![]() .
.
从而由正弦定理得sin B sin C=![]() sin A×
sin A×![]() sin A=
sin A=![]() sin2A=
sin2A=![]() ×
×![]() =
=![]() .
.


 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:高中数学 来源: 题型:
【题目】某民调机构为了了解民众是否支持英国脱离欧盟,随机抽调了100名民众,他们的年龄的频数及支持英国脱离欧盟的人数分布如下表:
年龄段 | 18-24岁 | 25-49岁 | 50-64岁 | 65岁及以上 |
频数 | 35 | 20 | 25 | 20 |
支持脱欧的人数 | 10 | 10 | 15 | 15 |
(Ⅰ)由以上统计数据填下面列联表,并判断是否有99%的把握认为以50岁胃分界点对是否支持脱离欧盟的态度有差异;
年龄低于50岁的人数 | 年龄不低于50岁的人数 | 合计 | |
支持“脱欧”人数 | |||
不支持“脱欧”人数 | |||
合计 |
附:![]()

(Ⅱ)若采用分层抽样的方式从18-64岁且支持英国脱离欧盟的民众中选出7人,再从这7人中随机选出2人,求这2人至少有1人年龄在18-24岁的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() ,如果满足:对任意
,如果满足:对任意![]() ,存在常数
,存在常数![]() ,都有
,都有![]() 成立,则称
成立,则称![]() 是
是![]() 上的有界函数,其中
上的有界函数,其中![]() 称为函数
称为函数![]() 的上界,已知函数
的上界,已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的值域,并判断函数
上的值域,并判断函数![]() 在
在![]() 上是否为有界函数,请说明理由;
上是否为有界函数,请说明理由;
(2)若函数![]() 在
在![]() 上是以4为上界的有界函数,求实数
上是以4为上界的有界函数,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,“共享单车”的出现为市民“绿色出行”提供了极大的方便,某共享单车公司“Mobike”计划在甲、乙两座城市共投资120万元,根据行业规定,每个城市至少要投资40万元,由前期市场调研可知:甲城市收益![]() 与投入
与投入![]() (单位:万元)满足
(单位:万元)满足![]() ,乙城市收益
,乙城市收益![]() 与投入
与投入![]() (单位:万元)满足
(单位:万元)满足![]() ,设甲城市的投入为
,设甲城市的投入为![]() (单位:万元),两个城市的总收益为
(单位:万元),两个城市的总收益为![]() (单位:万元)。
(单位:万元)。
(1)当甲城市投资50万元时,求此时公司总收益;
(2)试问如何安排甲、乙两个城市的投资,才能使总收益最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,
中, ![]() 的参数方程为
的参数方程为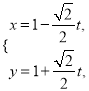 (
(![]() 为参数),在以坐标原点为极点,
为参数),在以坐标原点为极点, ![]() 轴正半轴为极轴的极坐标系中,
轴正半轴为极轴的极坐标系中, ![]() 的极坐标方程
的极坐标方程![]() .
.
(Ⅰ)说明![]() 是哪种曲线,并将
是哪种曲线,并将![]() 的方程化为普通方程;
的方程化为普通方程;
(Ⅱ)![]() 与
与![]() 有两个公共点
有两个公共点![]() ,顶点
,顶点![]() 的极坐标
的极坐标![]() ,求线段
,求线段![]() 的长及定点
的长及定点![]() 到
到![]() 两点的距离之积.
两点的距离之积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥PABCD的底面ABCD是矩形,PA⊥底面ABCD,点E、F分别是棱PC、PD的中点,则
①棱AB与PD所在直线垂直;
②平面PBC与平面ABCD垂直;
③△PCD的面积大于△PAB的面积;
④直线AE与直线BF是异面直线.
以上结论正确的是________.(写出所有正确结论的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,菱形ABCD的对角线AC与BD交于点O,点E,F分别在AD,CD上,AE=CF,EF交BD于点H.将△DEF沿EF折到△D′EF的位置.
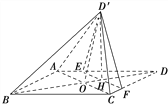
(1)证明:AC⊥HD′;
(2)若AB=5,AC=6,AE=![]() ,OD′=2
,OD′=2![]() ,求五棱锥D′ABCFE的体积.
,求五棱锥D′ABCFE的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】表示一位骑自行车和一位骑摩托车的旅行者在相距80 km的甲、乙两城间从甲城到乙城所行驶的路程与时间之间的函数关系,有人根据函数图象,提出了关于这两个旅行者的如下信息:

①骑自行车者比骑摩托车者早出发3 h,晚到1 h;
②骑自行车者是变速运动,骑摩托车者是匀速运动;
③骑摩托车者在出发1.5 h后追上了骑自行车者;
④骑摩托车者在出发1.5 h后与骑自行车者速度一样.
其中,正确信息的序号是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com