
【题目】如果,在![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 是
是![]() 内的一点.
内的一点.
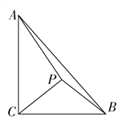
(1)若![]() 是等腰直角三角形
是等腰直角三角形![]() 的直角顶点,求
的直角顶点,求![]() 的长;
的长;
(2)若![]() ,设
,设![]() ,求
,求![]() 的面积
的面积![]() 的解析式,并求
的解析式,并求![]() 的最大值.
的最大值.
【答案】(1)PA=![]() (2)当θ=
(2)当θ=![]() 时,△PBC面积的最大值为
时,△PBC面积的最大值为![]()
【解析】试题分析: ![]() 根据题目条件求出
根据题目条件求出![]() 的大小,根据余弦定理即可求出
的大小,根据余弦定理即可求出![]() ;
;
![]() 在
在![]() 中,根据正弦定理,用含
中,根据正弦定理,用含![]() 的式子表达出
的式子表达出![]() ,
, ![]() ,然后根据
,然后根据
![]() ,可以求出
,可以求出![]() 的解析式,最后根据正弦函数的单调性,可以求出
的解析式,最后根据正弦函数的单调性,可以求出![]() 的最大值。
的最大值。
解析:(1)解法一:∵P是等腰直角三角形PBC的直角顶点,且BC=2,
∴∠PCB=![]() ,PC=
,PC=![]() ,又∵∠ACB=
,又∵∠ACB=![]() ,∴∠ACP=
,∴∠ACP=![]() ,
,
在△PAC中,由余弦定理得PA2=AC2+PC2-2AC·PCcos![]() =5,
=5,
∴PA=![]() .
.
(2)在△PBC中,∠BPC=![]() ,∠PCB=θ,
,∠PCB=θ,
∴∠PBC=![]() -θ,由正弦定理得
-θ,由正弦定理得![]() =
=![]() =
= ,
,
∴PB=![]() sinθ,PC=
sinθ,PC=![]()
![]() ,∴△PBC的面积S(θ)=
,∴△PBC的面积S(θ)=![]() PB·PCsin
PB·PCsin![]()
=![]()
![]() sinθ=2sinθcosθ-
sinθ=2sinθcosθ-![]() sin2θ=sin2θ+
sin2θ=sin2θ+![]() cos2θ-
cos2θ-![]()
=![]()
![]() -
-![]() ,θ∈
,θ∈![]() ,
,
∴当θ=![]() 时,△PBC面积的最大值为
时,△PBC面积的最大值为![]() .
.



 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案科目:高中数学 来源: 题型:
【题目】设数列{an}的各项都是正数,且对任意n∈N* , 都有(an﹣1)(an+3)=4Sn , 其中Sn为数列{an}的前n项和.
(1)求证数列{an}是等差数列;
(2)若数列{ ![]() }的前n项和为Tn , 求Tn .
}的前n项和为Tn , 求Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以原点为极点, ![]() 轴的正半轴为极轴,以相同的长度单位建立极坐标系,已知直线
轴的正半轴为极轴,以相同的长度单位建立极坐标系,已知直线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)设![]() 为参数,若
为参数,若![]() ,求直线
,求直线![]() 的参数方程;
的参数方程;
(2)已知直线![]() 与曲线
与曲线![]() 交于
交于![]() ,设
,设![]() ,且
,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地最近十年对某商品的需求量逐年上升,下表是部分统计数据:
年份 | 2008 | 2010 | 2012 | 2014 | 2016 |
需要量(万件) | 236 | 246 | 257 | 276 | 286 |
(1)利用所给数据求年需求量y与年份x之间的回归直线方程 ![]() =
= ![]() x+
x+ ![]() ;
;
(2)预测该地2018年的商品需求量(结果保留整数).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正方形ABCD的边长为1,弧BD是以点A为圆心的圆弧.
(1)在正方形内任取一点M,求事件“|AM|≤1”的概率;
(2)用大豆将正方形均匀铺满,经清点,发现大豆一共28粒,其中有22粒落在圆中阴影部分内,请据此估计圆周率π的近似值(精确到0.01). 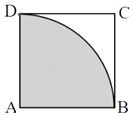
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】要测量底部不能到达的电视塔AB的高度,在C点测得塔顶A的仰角是45°,在D点测得塔顶A的仰角是30°,并测得水平面上的∠BCD=120°,CD=40m,则电视塔的高度为( ) 
A.40m
B.20m
C.305m
D.(20 ![]() ﹣40)m
﹣40)m
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】解答
(1)将一颗骰子(一种各个面上分别标有1,2,3,4,5,6个点的正方体玩具)先后抛掷2次,以分别得到的点数(m,n)作为点P的坐标(m,n),求:点P落在区域 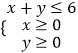 内的概率;
内的概率;
(2)在区间[1,6]上任取两个实数(m,n),求:使方程x2+mx+n2=0有实数根的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
以直角坐标系的原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立坐标系,已知点
轴的正半轴为极轴建立坐标系,已知点![]() 的直角坐标为
的直角坐标为![]() ,若直线
,若直线![]() 的极坐标方程为
的极坐标方程为![]() .曲线
.曲线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数).
为参数).
(1)求直线![]() 和曲线
和曲线![]() 的普通方程;
的普通方程;
(2)设直线![]() 和曲线
和曲线![]() 交于
交于![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com