
| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | 4 |
分析 设|MF1|=m,|MF2|=n,则m+n=4,又$\overrightarrow{M{F}_{1}}$•$\overrightarrow{M{F}_{2}}$=0,可得MF1⊥MF2,则m2+n2=(2c)2.
解答 解:由$\frac{x^2}{4}+{y^2}=1$,可得a=2,b=1,c=$\sqrt{3}$.
设|MF1|=m,|MF2|=n,则m+n=4,
又$\overrightarrow{M{F}_{1}}$•$\overrightarrow{M{F}_{2}}$=0,∴MF1⊥MF2,则m2+n2=(2c)2=12.
∴2mn=4,
∴△MF1F2的面积=$\frac{1}{2}mn$=1.
故选:A.
点评 本题考查了椭圆的定义标准方程、向量垂直与数量积的关系、三角形面积计算公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $-\frac{1}{2}$ | C. | 1或$-\frac{1}{2}$ | D. | -1或$-\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}{a^2}$ | B. | $\frac{1}{4}{a^2}$ | C. | $\frac{1}{8}{a^2}$ | D. | $\frac{{\sqrt{3}}}{8}{a^2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(a)+f(b)<2 f(1) | B. | f(a)+f(b)≤2 f(1) | C. | f(a)+f(b)≥2 f(1) | D. | f(a)+f(b)>2 f(1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
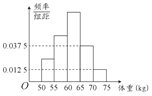 为了了解我校今年报考飞行员的学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,第2小组的频数为12,则报考飞行员的学生人数是( )
为了了解我校今年报考飞行员的学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,第2小组的频数为12,则报考飞行员的学生人数是( )| A. | 50 | B. | 47 | C. | 48 | D. | 52 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com