
设函数f(x)=x+ax2+blnx,曲线y=f(x)过P(1,0),且在P点处的切线斜率为2.
(1)求a,b的值;
(2)证明:f(x)≤2x-2.
(1) a=-1,b=3. (2)利用导数证明。
解析试题分析: (1)f ′(x)=1+2ax+ .(1分)
.(1分)
由已知条件得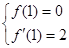 即
即
解得a=-1,b=3. (4分)
(2)f(x)的定义域为(0,+∞),
由(1)知f(x)=x-x2+3lnx.
设g(x)=f(x)-(2x-2)=2-x-x2+3lnx,则
g′(x)=-1-2x+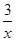 =-
=- . (6分)
. (6分)
当0<x<1时,g′(x)>0;当x>1时,g′(x)<0.
所以g(x)在(0,1)单调递增,在(1,+∞)单调递减.(8分)
而g(1)=0,故当x>0时,g(x)≤0,即f(x)≤2x-2. (10分)
考点:本题主要考查导数的几何意义,利用导数研究函数的单调性、最值,不等式组的证明。
点评:中档题,导数的应用是高考必考内容,思路往往比较明确根据导数值的正负,确定函数的单调性。定义不懂事的证明问题,往往通过构造函数,转化成求函数的最值,使问题得解。


科目:高中数学 来源: 题型:解答题
理科已知函数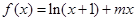 ,当
,当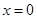 时,函数
时,函数 取得极大值.
取得极大值.
(Ⅰ)求实数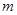 的值;(Ⅱ)已知结论:若函数
的值;(Ⅱ)已知结论:若函数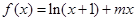 在区间
在区间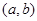 内导数都存在,且
内导数都存在,且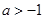 ,则存在
,则存在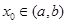 ,使得
,使得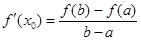 .试用这个结论证明:若
.试用这个结论证明:若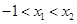 ,函数
,函数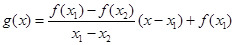 ,则对任意
,则对任意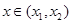 ,都有
,都有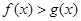 ;(Ⅲ)已知正数
;(Ⅲ)已知正数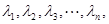 满足
满足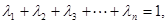 求证:当
求证:当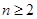 ,
,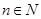 时,对任意大于
时,对任意大于 ,且互不相等的实数
,且互不相等的实数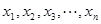 ,都有
,都有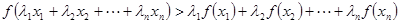
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数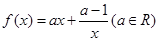 ,
, 。
。
(1)若对任意的实数a,函数 与
与 的图象在x = x0处的切线斜率总想等,求x0的值;
的图象在x = x0处的切线斜率总想等,求x0的值;
(2)若a > 0,对任意x > 0不等式 恒成立,求实数a的取值范围。
恒成立,求实数a的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com