
【题目】在平面直角坐标系xOy中,以O为极点,x轴的正半轴为极轴,建立极坐标系,曲线C的极坐标方程为![]() ;直线l的参数方程为
;直线l的参数方程为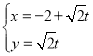 (t为参数).直线l与曲线C分别交于M,N两点.
(t为参数).直线l与曲线C分别交于M,N两点.
(1)写出曲线C的直角坐标方程和直线l的普通方程;
(2)若点P的极坐标为![]() ,
,![]() ,求
,求![]() 的值.
的值.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,已知抛物线![]()
![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 相交于
相交于![]() 两点,且当倾斜角为
两点,且当倾斜角为![]() 的直线
的直线![]() 经过抛物线
经过抛物线![]() 的焦点
的焦点![]() 时,有
时,有![]() .
.
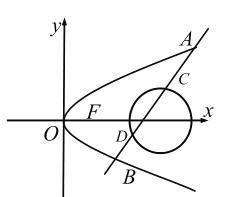
(1)求抛物线![]() 的方程;
的方程;
(2)已知圆![]() ,是否存在倾斜角不为
,是否存在倾斜角不为![]() 的直线
的直线![]() ,使得线段
,使得线段![]() 被圆
被圆![]() 截成三等分?若存在,求出直线
截成三等分?若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某幼儿园根据部分同年龄段的100名女童的身高数据绘制了频率分布直方图,其中身高的变化范围是[96,106](单位:厘米),样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106).
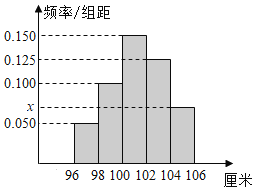
(1)求出![]() 的值,并求样本中女童的身高的众数和中位数,平均数;
的值,并求样本中女童的身高的众数和中位数,平均数;
(2)在身高在[100,102),[102,104),[104,106]的三组中,用分层抽样的方法抽取14名女童,则身高数据在[104,106]的女童中应抽取多少人数?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图为我国数学家赵爽![]() 约3世纪初
约3世纪初![]() 在为《周髀算经》作注时验证勾股定理的示意图,现在提供5种颜色给其中5个小区域涂色,规定每个区域只涂一种颜色,相邻区域颜色不同,则
在为《周髀算经》作注时验证勾股定理的示意图,现在提供5种颜色给其中5个小区域涂色,规定每个区域只涂一种颜色,相邻区域颜色不同,则![]() 区域涂色不相同的概率为
区域涂色不相同的概率为![]()
![]()

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,求实数
,求实数![]() 、
、![]() 的值;
的值;
(2)设函数![]() ,
,![]() (其中
(其中![]() 为自然对数的底数).
为自然对数的底数).
①当![]() 时,求
时,求![]() 的最大值;
的最大值;
②若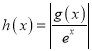 是单调递减函数,求实数
是单调递减函数,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,且
,且![]() ,椭圆经过点
,椭圆经过点![]() .
.
(1)求椭圆的方程;
(2)直线![]() 过椭圆右顶点
过椭圆右顶点![]() ,交椭圆于另一点
,交椭圆于另一点![]() ,点
,点![]() 在直线
在直线![]() 上,且
上,且![]() .若
.若![]() ,求直线
,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年10月1日,庆祝中华人民共和国成立70周年大会、阅兵式、群众游行在北京隆重举行,这次阅兵编59个方(梯)队和联合军乐团,总规模约1.5万人,各型飞机160余架、装备580余套,是近几次阅兵中规模最大的一次.某机构统计了观看此次阅兵的年龄在30岁至80岁之间的100个观众,按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.

(1)求![]() 的值及这100个人的平均年龄(同一组中的数据用该组区间的中点值为代表);
的值及这100个人的平均年龄(同一组中的数据用该组区间的中点值为代表);
(2)用分层抽样的方法在年龄为![]() 、
、![]() 的人中抽取5人,再从抽取的5人中随机抽取2人接受采访,求接受采访的2人中年龄在
的人中抽取5人,再从抽取的5人中随机抽取2人接受采访,求接受采访的2人中年龄在![]() 的恰有1人的概率.
的恰有1人的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com