
| x | 100 |
| x |
| 5 |
| x |
| 100 |
| 1000 |
| 100 |
| x |
| 5 |
| 4lge |
| x |
| 1 |
| 5 |
| 4lge |
| x |
| 1 |
| 5 |
| 4lge |
| 10 |
| 1 |
| 5 |
| lge2-1 |
| 5 |
| x |
| 5 |


 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案科目:高中数学 来源: 题型:
| x | 150 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x |
| 150 |
| 10x-3a |
| x+2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x |
| 150 |
| 10x-3a |
| x+2 |
查看答案和解析>>
科目:高中数学 来源:2014届福建省高二下学期期末考试文科数学试卷(解析版) 题型:解答题
某公司拟投资开发某种新能源产品,估计能获得10万元至1000万元的投资收益.为加快开发进程,特制定了产品研制的奖励方案:奖金 (万元)随投资收益
(万元)随投资收益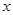 (万元)的增加而增加,但奖金总数不超过9万元,同时奖金不超过投资收益的20%.
(万元)的增加而增加,但奖金总数不超过9万元,同时奖金不超过投资收益的20%.
现给出两个奖励模型:①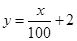 ;②
;②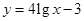 .
.
试分析这两个函数模型是否符合公司要求?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com