[3,+∞)
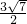
1
分析:A. 由已知条件利用绝对值不等式的性质可得|x+1|+|x-2|≥3,结合题意可得a≥3.
B.结合线割线定理,我们可以求出DB的长,再由△DBC∽△DCA根据相似三角形的性质可以求出AC的长.
C.把极坐标方程化为直角坐标方程,求出圆心到直线的距离,将此距离和圆的半径作对比,得出结论.
解答:A.∵|x+1|+|x-2|≥|(x+1)-(x-2)|=3,即|x+1|+|x-2|≥3,
由关于x的不等式|x+1|+|x-2|≤a有解,知a≥3,
故答案为[3,+∞).
B.由切割线定理得:DB•DA=DC
2,即DB(DB+BA)=DC
2,∴DB
2+3DB-28=0,得DB=4.
∵∠A=∠BCD,∴△DBC∽△DCA,∴
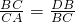
,解得AC=
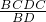
=
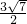
.
故答案为
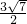
.
C.直线ρcos(θ-

)=

即

ρcosθ+

ρsinθ=

,化为直角坐标方程为 x+y-2=0,
圆ρ=2 即 x
2+y
2=4,圆心到直线的距离等于
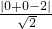
=

<2(半径),
故直线和圆相交,故直线和圆有两个交点,
故答案为 2.
点评:本题主要考查绝对值不等式、有关绝对值不等式恒成立的问题.与圆有关的比例线段,相似三角形的性质.把极坐标方程化为直角坐标方程的方法,点到直线的距离公式的应用,属于中档题.

 (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
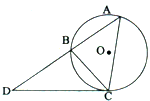
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)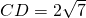 ,AB=BC=3,则AC长________.
,AB=BC=3,则AC长________. 与圆
与圆 的公共点个数是________.
的公共点个数是________.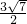 1
1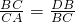 ,解得AC=
,解得AC=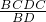 =
=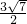 .
.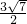 .
. )=
)= 即
即  ρcosθ+
ρcosθ+ ρsinθ=
ρsinθ= ,化为直角坐标方程为 x+y-2=0,
,化为直角坐标方程为 x+y-2=0,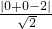 =
= <2(半径),
<2(半径),

 (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分) (三选一,考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
(三选一,考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分) (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分) (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)