【题目】已知函数
.
（1）若
，求函数
的值域；
（2）讨论函数的奇偶性，并说明理由.
【答案】（1）
； （2）当
时，函数
为偶函数；当
时，函数是奇函数；当
且
，函数既不是奇函数，也不是偶函数．.
【解析】
（1）将代入函数解析式，求得函数的定义域，将函数解析式化简，之后借助于指数函数的值域以及不等式的性质求得结果；
（2）分类讨论，利用奇偶函数的定义，讨论函数的奇偶性，从而求得结果.
（1）当 时，定义域为
，
，
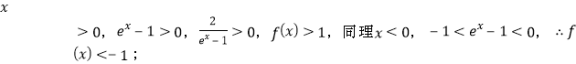
所以值域为
（2）①当时，
定义域为R，故函数
为偶函数；
②当且时，定义域为
不关于原点对称，故函数既不是奇函数，也不是偶函数 ；
③当时，
定义域为
故函数是奇函数；
④当
时，定义域为R关于原点对称，若是奇函数 
当
时，
故函数是奇函数；
若是偶函数
且
时，，函数既不是奇函数，也不是偶函数．
综上：
当时，函数为偶函数；
当 
时，函数是奇函数；
当 且 
，函数既不是奇函数，也不是偶函数．
寒假天地重庆出版社系列答案科目：高中数学 来源： 题型：
【题目】已知函数f（x）= 
（b∈R）．若存在x∈[ 
，2]，使得f（x）+xf′（x）＞0，则实数 b的取值范围是（ ）
A.（﹣∞， 
）
B.（﹣∞， 
）
C.（﹣∞，3）
D.（﹣∞， 
）
查看答案和解析>>
科目：高中数学 来源： 题型：
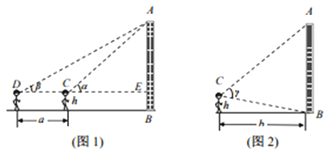
【题目】某校高一数学研究小组测量学校的一座教学楼AB的高度
已知测角仪器距离地面的高度为h米，现有两种测量方法：
方法
如图
用测角仪器，对准教学楼的顶部A，计算并记录仰角
；
后退a米，重复
中的操作，计算并记录仰角
．
方法
如图
用测角仪器，对准教学楼的顶部A底部B，测出教学楼的视角
，测试点与教学楼的水平距离b米．
请你回答下列问题：
用数据
，
，a，h表示出教学楼AB的高度；
按照方法II，用数据
，b，h表示出教学楼AB的高度．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下面说法中错误的是（ ）
A. 经过定点
的直线都可以用方程
表示
B. 经过定点的直线都可以用方程
表示
C. 经过定点
的直线都可以用方程
表示
D. 不经过原点的直线都可以用方程
表示
E. 经过任意两个不同的点
，
的直线都可以用方程
表示
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知数列{an}为等差数列，a3=5，a7=13，数列{bn}的前n项和为Sn ， 且有Sn=2bn﹣1．
（1）求{an}、{bn}的通项公式；
（2）若cn=anbn ， {cn}的前n项和为Tn ， 求Tn ．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】
，
为两个不同的平面，
，
为两条不同的直线，下列命题中正确的是（ ）
①若
，
，则
； ②若
，
，则
；
③若
，
，
，则
④若
，
，
，则.
A. ①③ B. ①④ C. ②③ D. ②④
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知圆心为
的圆，满足下列条件：圆心位于
轴正半轴上，与直线
相切，且被
轴截得的弦长为
，圆的面积小于13.
（1）求圆的标准方程；
（2）若点
，点
是圆上一点，点
是
的重心，求点的轨迹方程；
（3）设过点
的直线
与圆交于不同的两点
，
，以
，
为邻边作平行四边形
.是否存在这样的直线，使得直线
与
恰好平行？如果存在，求出的方程；如果不存在，请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】分形几何学是美籍法国数学家伯努瓦
曼德尔布罗特（
）在20世纪70年代创立的一门新学科，它的创立为解决传统众多领域的难题提供了全新的思路.下图是按照分型的规律生长成的一个树形图，则第10行的空心圆的个数是__________．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
