练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某工厂生产某种产品，每日的成本C（单位：万元）与日产量x（单位：吨）满足函数关系式C=4+x，每日的销售额S（单位：万元）与日产量x满足函数关系式

    S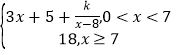＝，已知每日的利润L=S﹣C，且当x=4时，L=7．

    （1）求k；

    （2）当日产量为多少吨时，每日的利润可以达到最大？并求此最大值．

    【答案】（1）；（2）日产量为吨时，日利润达到最大万元.

    【解析】

    （1）利用每日的利润L＝S﹣C，且当x＝4时，L＝7，可求k的值；

    （2）利用分段函数，分别求出相应的最值，即可得出函数的最大值．

    （1）利润，

    当时，，所以，

    ，解得：。

    （2）当时，为单调递减函数，

    所以，当时，最大利润

    当时， ，

    当时，最大利润

    综上可知，当日产量为5吨时，日利润达到最大9万元

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图1为某省2018年1~4月快递业务量统计图，图2是该省2018年1~4月快递业务收入统计图，下列对统计图理解错误的是（ ）

    A. 2018年1~4月的业务量，3月最高，2月最低，差值接近2000万件

    B. 2018年1~4月的业务量同比增长率均超过50%，在3月底最高

    C. 从两图来看，2018年1~4月中的同一个月的快递业务量与收入的同比增长率并不完全一致

    D. 从1~4月来看，该省在2018年快递业务收入同比增长率逐月增长

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=1-（a＞0且a≠1）是定义在（-∞，+∞）上的奇函数．

    （1）求a的值；

    （2）证明：函数f（x）在定义域（-∞，+∞）内是增函数；

    （3）当x∈（0，1]时，tf（x）≥2x-2恒成立，求实数t的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知直线被圆截得的弦长为.

    (1)求的值；

    (2)求过点并与圆C相切的直线方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在直四棱柱中，已知，．

    （1）求证：；

    （2）设是上一点，试确定的位置，使平面，并说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】用红、黄、蓝三种不同的颜色给大小相同的三个圆随机涂色，每个圆只涂一种颜色.设事件“三个圆的颜色全不相同”，事件“三个圆的颜色不全相同”，事件“其中两个圆的颜色相同”，事件“三个圆的颜色全相同”.

    （1）写出试验的样本空间.

    （2）用集合的形式表示事件.

    （3）事件与事件有什么关系？事件和的交事件与事件有什么关系？并说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在边长为2菱形ABCD中，，且对角线AC与BD交点为O．沿BD将折起，使点A到达点的位置．

    （1）若，求证：平面ABCD；

    （2）若，求三棱锥体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，直三棱柱中， 是的中点.

    （1）证明： 平面；

    （2）若， ，求点到平面的距离.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某种产品的质量以其质量指标值来衡量．当时，产品为一等品；当时，产品为二等品；当时，产品为三等品．现从甲、乙两条生产线，各随机抽取了100件该产品作为样本，测量每件产品的质量指标值，整理得到甲、乙两条生产线产品的质量指标值的频率分布直方图如图所示，视样本的频率为总体的概率．

    （1）若从甲、乙生产线生产的产品中各随机抽取1件，求恰好抽到1件一等品的概率；

    （2）若一件三等品、二等品、一等品的利润分别为10元、20元、30元，从乙生产线生产的产品中随机抽取2件，求这两件产品的利润之和的分布列和数学期望；

    （3）若从甲生产线生产的产品中随机抽取件，其中抽到二等品的件数为随机变量，且的数学期望不小于1200，求的最小值．

    查看答案和解析>>

    同步练习册答案