
【题目】设函数![]() 满足
满足![]() 且
且![]() .
.
(1)求证![]() ,并求
,并求![]() 的取值范围;
的取值范围;
(2)证明函数![]() 在
在![]() 内至少有一个零点;
内至少有一个零点;
(3)设![]() 是函数
是函数![]() 的两个零点,求
的两个零点,求![]() 的取值范围.
的取值范围.
【答案】(1)详见解析,(2)详见解析,(3)![]() .
.
【解析】
试题分析:(1)由等量关系消去C是解题思路,揭示a为正数是解题关键,本题是典型题,实质是三个实数和为零,则最大的数必为正数,最小的数必为负数,中间的数不确定,通常被消去,(2)证明区间内有解首选零点存在定理.连续性不是高中数学考核的知识点,重点考核的是区间端点函数值的符号.要确定区间端点函数值的符号,需恰当选择区间端点,这是应用零点存在定理的难点,本题![]() 符号确定,但
符号确定,但![]() 符号不确定.由于两者符号与
符号不确定.由于两者符号与![]() 有关,所以需要对
有关,所以需要对![]() 进行讨论,(3)要求
进行讨论,(3)要求![]() 的取值范围,需先运用韦达定理建立
的取值范围,需先运用韦达定理建立![]() 函数解析式(二次函数),再利用(1)的范围(定义域),求二次函数值域.本题思路简单,但不能忽视定义域在解题中作用.
函数解析式(二次函数),再利用(1)的范围(定义域),求二次函数值域.本题思路简单,但不能忽视定义域在解题中作用.
试题解析:(1)由题意得![]() ,
,![]()
又![]() ,
,![]() 2分
2分
由![]() ,得
,得![]()
![]() ,
,![]() ,得
,得![]() 5分
5分
(2)![]() ,
,![]()
又![]() ,
,![]()
若![]() 则
则![]() ,
,![]() 在
在![]() 上有零点;
上有零点;
若![]() 则
则![]() ,
,![]() 在
在![]() 上有零点
上有零点
![]() 函数
函数![]() 在
在![]() 内至少有一个零点 9分
内至少有一个零点 9分
(3)![]()
![]()
![]()
![]() ,
,![]() 13分
13分


科目:高中数学 来源: 题型:
【题目】已知以点A(-1,2)为圆心的圆与直线l1:x+2y+7=0相切.过点B(-2,0)的动直线l与圆A相交于M,N两点,Q是MN的中点.
(1)求圆A的方程;
(2)当|MN|=2![]() 时,求直线l的方程.
时,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图, ![]() 是边长为
是边长为 ![]() 的正方形,
的正方形, ![]() 平面
平面 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 与平面
与平面 ![]() 所成角为
所成角为 ![]() .
.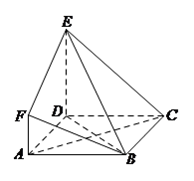
(Ⅰ)求证: ![]() 平面
平面 ![]() .
.
(Ⅱ)求二面角 ![]() 的余弦值.
的余弦值.
(Ⅲ)设点 ![]() 是线段
是线段 ![]() 上一个动点,试确定点
上一个动点,试确定点 ![]() 的位置,使得
的位置,使得 ![]() 平面
平面 ![]() ,并证明你的结论.
,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sinx,若存在x1 , x2 , ,xm满足0≤x1<x2<xm≤6π,且|f(x1)﹣f(x2)|+|f(x2)﹣f(x3)|+|f(xn﹣1)﹣f(xn)|=12,(m≥2,m∈N*),则m的最小值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且满足Sn=2an﹣2;数列{bn}的前n项和为Tn , 且满足b1=1,b2=2, ![]() .
.
(1)求数列{an}、{bn}的通项公式;
(2)是否存在正整数n,使得 ![]() 恰为数列{bn}中的一项?若存在,求所有满足要求的bn;若不存在,说明理由.
恰为数列{bn}中的一项?若存在,求所有满足要求的bn;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经过市场调查,某种商品在销售中有如下关系:第![]() 天的销售价格(单位:元/件)为
天的销售价格(单位:元/件)为![]() ,第
,第![]() 天的销售量(单位:件)为
天的销售量(单位:件)为![]() (
(![]() 为常数),且在第20天该商品的销售收入为1200元(
为常数),且在第20天该商品的销售收入为1200元(![]() ).
).
(Ⅰ)求![]() 的值,并求第15天该商品的销售收入;
的值,并求第15天该商品的销售收入;
(Ⅱ)求在这30天中,该商品日销售收入![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】集合![]() 由满足以下性质的函数
由满足以下性质的函数![]() 组成:①
组成:①![]() 在
在![]() 上是增函数;②对于任意的
上是增函数;②对于任意的![]() ,
, ![]() .已知函数
.已知函数![]() ,
, ![]() .
.
(1)试判断![]() ,
, ![]() 是否属于集合
是否属于集合![]() ,并说明理由;
,并说明理由;
(2)将(1)中你认为属于集合![]() 的函数记为
的函数记为![]() .
.
(ⅰ)试用列举法表示集合![]() ;
;
(ⅱ)若函数![]() 在区间
在区间![]() 上的值域为
上的值域为![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】相传古代印度国王在奖赏他聪明能干的宰相达依尔(国际象棋发明者)时,问他需要什么,达依尔说:“国王只要在国际象棋棋盘的第一格子上放一粒麦子,第二格子上放二粒,第三格子上放四粒,以后按比例每一格加一倍,一直放到第64格(国际象棋棋盘格数是8×8=64),我就感恩不尽,其他什么也不要了.”国王想:“这才有多少,还不容易!”于是让人扛来一袋小麦,但不到一会儿就用完了,再来一袋很快又没有了,结果全印度的粮食用完还不够,国王很奇怪,怎么也算不清这笔账.请你设计一个程序框图表示其算法,来帮国王计算一下需要多少粒小麦.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com