
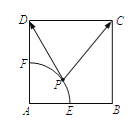
【题目】如图,已知正方形![]() 的边长为2,点
的边长为2,点![]() 为
为![]() 的中点.以
的中点.以![]() 为圆心,
为圆心,![]() 为半径,作弧交
为半径,作弧交![]() 于点
于点![]() .若
.若![]() 为劣弧
为劣弧![]() 上的动点,则
上的动点,则![]() 的最小值为__________.
的最小值为__________.
科目:高中数学 来源: 题型:
【题目】对于定义域为![]() 的函数
的函数![]() ,如果同时满足以下三条:①对任意的
,如果同时满足以下三条:①对任意的![]() ,总有
,总有![]() ;②
;②![]() ;③若
;③若![]() ,都有
,都有![]() 成立,则称函数
成立,则称函数![]() 为理想函数.
为理想函数.
(1) 若函数![]() 为理想函数,求
为理想函数,求![]() 的值;
的值;
(2)判断函数![]()
![]() 是否为理想函数,并予以证明;
是否为理想函数,并予以证明;
(3) 若函数![]() 为理想函数,
为理想函数,![]() 假定
假定![]()
![]() ,使得
,使得![]() ,且
,且![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=aexlnx+ ![]() ,曲线y=f(x)在点(1,f(1))处得切线方程为y=e(x﹣1)+2.
,曲线y=f(x)在点(1,f(1))处得切线方程为y=e(x﹣1)+2.
(1)求a、b;
(2)证明:f(x)>1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() +
+ ![]() =1(a>b>0)的右焦点为(
=1(a>b>0)的右焦点为( ![]() ,0),离心率为
,0),离心率为 ![]() .
.
(1)求椭圆C的标准方程;
(2)若动点P(x0 , y0)为椭圆C外一点,且点P到椭圆C的两条切线相互垂直,求点P的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() (c为常数),且f(1)=0.
(c为常数),且f(1)=0.
(1)求c的值;
(2)证明函数f(x)在[0,2]上是单调递增函数;
(3)已知函数g(x)=f(ex),判断函数g(x)的奇偶性.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经过市场调查,某种商品在销售中有如下关系:第x(1≤x≤30,x∈N+)天的销售价格(单位:元/件)为f(x)=![]() 第x天的销售量(单位:件)为g(x)=a-x(a为常数),且在第20天该商品的销售收入为1 200元(销售收入=销售价格×销售量).
第x天的销售量(单位:件)为g(x)=a-x(a为常数),且在第20天该商品的销售收入为1 200元(销售收入=销售价格×销售量).
(1)求a的值,并求第15天该商品的销售收入;
(2)求在这30天中,该商品日销售收入y的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2014福建)在下列向量组中,可以把向量 ![]() =(3,2)表示出来的是( )
=(3,2)表示出来的是( )
A.![]() =(0,0),
=(0,0), ![]() =(1,2)
=(1,2)
B.![]() =(﹣1,2),
=(﹣1,2), ![]() =(5,﹣2)
=(5,﹣2)
C.![]() =(3,5),
=(3,5), ![]() =(6,10)
=(6,10)
D.![]() =(2,﹣3),
=(2,﹣3), ![]() =(﹣2,3)
=(﹣2,3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线E: ![]() ﹣
﹣ ![]() =1(a>0,b>0)的两条渐近线分别为l1:y=2x,l2:y=﹣2x.
=1(a>0,b>0)的两条渐近线分别为l1:y=2x,l2:y=﹣2x. 
(1)求双曲线E的离心率;
(2)如图,O为坐标原点,动直线l分别交直线l1 , l2于A,B两点(A,B分别在第一、第四象限),且△OAB的面积恒为8,试探究:是否存在总与直线l有且只有一个公共点的双曲线E?若存在,求出双曲线E的方程,若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com