
【题目】已知命题p:x∈R,x2+2x﹣m=0;命题q:x∈R,mx2+mx+1>0.
(1)若命题p为真命题,求实数m的取值范围;
(2)若命题q为假命题,求实数m的取值范围;
(3)若命题p∨q为真命题,且p∧q为假命题,求实数m的取值范围.
【答案】
(1)解:若命题p为真命题,则x2+2x﹣m=0有实数根,
∴△=4+4m≥0,解得:m≥﹣1,
即m的取值范围为[﹣1,+∞);
(2)解:若命题q为假命题,则
①m=0时,不合题意;
②m>0时,△=m2﹣4m≥0,解得:m≥4;
③m<0时,符合题意.
综上:实数m的取值范围为(﹣∞,0)∪[4,+∞).
(3)解:由(1)得p为真命题时,m≥﹣1;p为假命题时,m<﹣1,
由(2)得q为真命题时,0≤m<4;q为假命题时,m<0或m≥4,
∵p∨q为真命题,且p∧q为假命题,∴“p真,q假”或“p假,q真”
∴ ![]() 或
或 ![]() ,
,
解得实数m的取值范围为[﹣1,0)∪[4,+∞).
【解析】(1)若命题p为真命题,则x2+2x﹣m=0有实数根,根据△≥0,解出即可;(2)若命题q为假命题,通过讨论(1)m=0时,(2)m>0时,(3)m<0时的情况,从而得到答案.(3)通过讨论“p真,q假”或“p假,q真”的情况,得到不等式组,解出即可.
【考点精析】认真审题,首先需要了解复合命题的真假(“或”、 “且”、 “非”的真值判断:“非p”形式复合命题的真假与F的真假相反;“p且q”形式复合命题当P与q同为真时为真,其他情况时为假;“p或q”形式复合命题当p与q同为假时为假,其他情况时为真),还要掌握全称命题(全称命题![]() :
:![]() ,
,![]() ,它的否定
,它的否定![]() :
:![]() ,
,![]() ;全称命题的否定是特称命题)的相关知识才是答题的关键.
;全称命题的否定是特称命题)的相关知识才是答题的关键.


科目:高中数学 来源: 题型:
【题目】函数f(x)=|sinx+cosx|+|sinx﹣cosx|是( )
A.最小正周期为π的奇函数
B.最小正周期为π的偶函数
C.最小正周期为 ![]() 的奇函数
的奇函数
D.最小正周期为 ![]() 的偶函数
的偶函数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(x﹣1)|x﹣a|﹣x﹣2a(x∈R).
(1)若a=﹣1,求方程f(x)=1的解集;
(2)若 ![]() ,试判断函数y=f(x)在R上的零点个数,并求此时y=f(x)所有零点之和的取值范围.
,试判断函数y=f(x)在R上的零点个数,并求此时y=f(x)所有零点之和的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】雾霾是人体健康的隐形杀手,爱护环境,人人有责.某环保实验室在雾霾天采用清洁剂处理教室空气质量.实验发现,当在教室释放清洁剂的过程中,空气中清洁剂的含剂浓度y(mg/m3)与时间t(h)成正比;释放完毕后,y与t的函数关系为y=( ![]() )t﹣a(a为常数),如图,已知当教室的空气中含剂浓度在0.25mg/m3以上时,教室最适合人体活动.根据图中信息,从一次释放清洁剂开始,这间教室有h最适合人体活动.
)t﹣a(a为常数),如图,已知当教室的空气中含剂浓度在0.25mg/m3以上时,教室最适合人体活动.根据图中信息,从一次释放清洁剂开始,这间教室有h最适合人体活动. 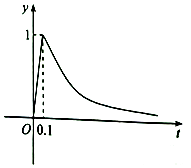
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题p:函数f(x)=lg(ax2﹣x+ ![]() )的定义域为R;命题q:不等式3x﹣9x<a对一切正实数x均成立.如果“p或q”为真命题,“p且q”为假命题,求实数a的取值范围.
)的定义域为R;命题q:不等式3x﹣9x<a对一切正实数x均成立.如果“p或q”为真命题,“p且q”为假命题,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=5|x|﹣ ![]() ,则使得f(2x+1)>f(x)成立的x取值范围是( )
,则使得f(2x+1)>f(x)成立的x取值范围是( )
A.(﹣1,﹣ ![]() )
)
B.(﹣3,﹣1)
C.(﹣1,+∞)
D.(﹣∞,﹣1)∪(﹣ ![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD﹣A1B1C1D1中,E,F分别是棱AB、BC的中点,则平面A1DE与平面C1DF所成二面角的余弦值为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知全集U=R,集合A={x|0<log2x<2},B={x|x≤3m﹣4或x≥8+m}(m<6).
(1)若m=2,求A∩(UB);
(2)若A∩(UB)=,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com