(文科做):已知双曲线过点A(-2,4)和B(4,4),它的一个焦点是抛物线y2=4x的焦点,求它的另一个焦点的轨迹方程.
解:∵抛物线y
2=4x的焦点坐标为(1,0),
∴不妨设双曲线的焦点F
1(1,0),
∵双曲线过点A(-2,4)和B(4,4),
∴|AF
1|=|BF
1|=5,
由双曲线的定义知,||AF
1|-|AF
2||=||BF
1|-|BF
2||,即|5-|AF
2||=|5-|BF
2||,
(1)当5-|AF
2|=5-|BF
2|时,即|AF
2|=|BF
2|,
∴焦点F
2的轨迹是线段AB的中垂线,其方程为x=1(y≠0),
(2)当5-|AF
2|=|BF
2|-5时,即|AF
2|+|BF
2|=10>6,
∴焦点F
2的轨迹是以A、B为焦点,长轴为10的椭圆,
∴其中心是(1,4),a=5,c=3,∴b
2=25-9=16,
其方程为
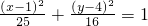
(y≠0).
∴所求的轨迹方程为:x=1(y≠0)或
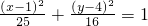
(y≠0).
分析:先求出抛物线y
2=4x的焦点坐标为(1,0),再由双曲线的定义列出有关另一个焦点的方程,再进行分类讨论,由式子的几何意义和椭圆的定义进行求解,并把不符合题意的点去掉.
点评:本题考查了抛物线的性质,以及由双曲线和椭圆的定义求动点的轨迹方程,要求学生具备一定的逻辑推理能力,具有较大的综合性.

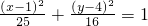 (y≠0).
(y≠0).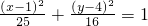 (y≠0).
(y≠0).
