练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    (本小题满分14分)为了解初三学生女生身高情况，某中学对初三女生身高进行了一次抽样调查，根据所得数据整理后列出了频率分布表如下：
    组　别       频数   频率   
    145.5～149.5      1       0.02   
    149.5～153.5      4       0.08   
    153.5～157.5    22     0.44   
    157.5～161.5      13      0.26   
    161.5～165.5      8       0.16   
    165.5～169.5     m       n  
    合　计        M       N  
    （1）求出表中所表示的数m,n,M,N分别是多少？
    （2）画出频率分布直方图和频率分布折线图.
    （3）若要从中再用分层抽样方法抽出10人作进一步调查，则身高在[153.5，161.5）范围内的应抽出多少人？
    （4）根据频率分布直方图，分别求出被测女生身高的众数，中位数和平均数？（结果保留一位小数）

    （1）    ；（2）见解析；
    （3）7人；（4）众数：155.5   中位数：157.1    平均数：157.8。

    解析

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    （本题满分12分）
    已知函数（ ）
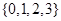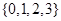    (1)若从集合中任取一个元素，从集合中任取一个元素，求方程恰有两个不相等实根的概率；
    (2)若从区间中任取一个数，从区间中任取一个数，求方程没有实根的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （本题满分12分）一个口袋内装有大小相同的6个小球，其中2个红球，记为A1、A2，4个黑球，记为B1、B2、B3、B4，从中一次摸出2个球.
    （Ⅰ）写出所有的基本事件；
    （Ⅱ）求摸出的两个球颜色不同的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （本小题满分13分）把一个正方体的表面涂上红色，在它的长、宽、高上等距离地各切三刀，则大正方体被分割成64个大小相等的小正方体，将这些小正方体均匀地搅混在一起，如果从中任取1个，求下列事件的概率
    （1）事件A＝“这个小正方体各个面都没有涂红色”
    （2）事件B＝“这个小正方体只有1个面涂红色”
    （3）事件C＝“这个小正方体至少2个面涂红色”

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知、两个盒子中分别装有标记为，，，的大小相同的四个小球，甲从盒中等可能地取出个球，乙从盒中等可能地取出个球．
    （1）用有序数对表示事件“甲抽到标号为i的小球，乙抽到标号为是j的小球”，求取出的两球标号之和为5的概率；
    （2）甲、乙两人玩游戏，约定规则：若甲抽到的小球的标号比乙大，则甲胜；反之，则乙胜．你认为此规则是否公平？请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （本小题满分12分）
    在一次数学考试中，第21题和第22题为选做题. 规定每位考生必须且只须在其中选做一题. 设4名考生选做每一道题的概率均为.
    （1）求其中甲、乙两名学生选做同一道题的概率；
    （2）设这4名考生中选做第22题的学生个数为，求的概率分布及数学期望. 的解析

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （本小题满分13分）为增强市民交通规范意识，我市面向全市征召劝导员志愿者，分布于各候车亭或十字路口处．现从符合条件的500名志愿者中随机抽取100名志愿者，他们的年龄情况如下表所示．
    （1）频率分布表中的①、②位置应填什么数据？并在答题卡中补全频率分布直方图（如图），再根据频率分布直方图估计这500名志愿者中年龄在[30，35)岁的人数；
    （2）在抽出的100名志愿者中按年龄再采用分层抽样法抽取20人参加“规范摩的司机的交通意识”培训活动，从这20人中选取2名志愿者担任主要负责人，记这2名志愿者中“年龄低于30岁”的人数为X，求X的分布列及数学期望．

    分组（单位：岁）
         		频数
         		频率
     
    [20，25)
         		5
         		0.05
     
    [25，30)
         		①
         		0.20
     
    [30，35)
         		35
         		②
     
    [35，40)
         		30
         		0.30
     
    [40，45]
         		10
         		0.10
     
    合计
         		100
         		1.00
     
     

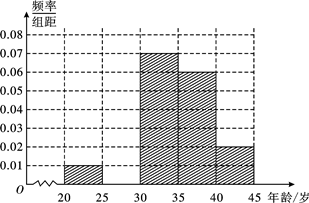
    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （本大题9分）袋中有2个红球，n个白球，各球除颜色外均相同.已知从袋中摸出2个球均为白球的概率为，（Ⅰ）求n；（Ⅱ）从袋中不放回的依次摸出三个球，记ξ为相邻两次摸出的球不同色的次数（例如：若取出的球依次为红球、白球、白球，则ξ=1），求随机变量ξ的分布列及其数学期望Eξ.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题


    （14分）（理）袋中装有黑球和白球共7个,从中任取2个球都是白球的概率为现有甲、乙两人从袋中轮流摸取1球，甲先取，乙后取，然后甲再取……取后不放回，直到两人中有一人取到白球时既终止，每个球在每一次被取出的机会是等可能的，用表示取球终止所需要的取球次数．
    （I）求袋中所有的白球的个数；
    （II）求随机变量的概率分布；
    （III）求甲取到白球的概率．

    查看答案和解析>>

    同步练习册答案