
【题目】今年年初,中共中央、国务院发布《关于开展扫黑除恶专项斗争的通知》,在全国范围部署开展扫黑除恶专项斗争.那么这次的“扫黑除恶”专项斗争与2000年、2006年两次在全国范围内持续开展了十多年的“打黑除恶”专项斗争是否相同呢?某高校一个社团在年后开学后随机调查了![]() 位该校在读大学生,就“扫黑除恶”与“打黑除恶”是否相同进行了一次调查,得到具体数据如表:
位该校在读大学生,就“扫黑除恶”与“打黑除恶”是否相同进行了一次调查,得到具体数据如表:
不相同 | 相同 | 合计 | |
男 |
|
|
|
女 |
|
|
|
合计 |
|
|
|
(1)根据如上的![]() 列联表,能否在犯错误的概率不超过
列联表,能否在犯错误的概率不超过![]() 的前提下,认为“扫黑除恶”与“打黑除恶”是否相同与性别有关"?
的前提下,认为“扫黑除恶”与“打黑除恶”是否相同与性别有关"?
(2)计算这![]() 位大学生认为“扫黑除恶”与“打黑除恶”不相同的频率,并据此估算该校
位大学生认为“扫黑除恶”与“打黑除恶”不相同的频率,并据此估算该校![]() 名在读大学生中认为“扫黑除恶”与“打黑除恶”不相同的人数;
名在读大学生中认为“扫黑除恶”与“打黑除恶”不相同的人数;
(3)为了解该校大学生对“扫黑除恶”与“打黑除恶”不同之处的知道情况,该校学生会组织部选取![]() 位男生和
位男生和![]() 位女生逐个进行采访,最后再随机选取
位女生逐个进行采访,最后再随机选取![]() 次采访记录放到该大学的官方网站上,求最后被选取的
次采访记录放到该大学的官方网站上,求最后被选取的![]() 次采访对象中至少有一位男生的概率.
次采访对象中至少有一位男生的概率.
参考公式:![]()
![]() .
.
附表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
【答案】(1)不能在犯错误的概率不超过![]() 的前提下,认为““扫黑除恶”与“打黑除恶”是否相同与性别有关”;(2)
的前提下,认为““扫黑除恶”与“打黑除恶”是否相同与性别有关”;(2)![]() 人;(3)
人;(3)![]() 。
。
【解析】
(1)计算观测值k2,即可得出结论;(2)由图表中的数据计算不相同的频率, 据此估算该校![]() 名在读大学生不相同的人数;(3)根据古典概型求概率的方法即可求出.
名在读大学生不相同的人数;(3)根据古典概型求概率的方法即可求出.
(1)根据列联表中的数据,得到![]() 的观测值为
的观测值为![]()
故不能在犯错误的概率不超过![]() 的前提下,认为““扫黑除恶”与“打黑除恶”是否相同与性别有关”。
的前提下,认为““扫黑除恶”与“打黑除恶”是否相同与性别有关”。
(2)这![]() 位大学生认为“扫黑除恶”与“打黑除恶”不相同的频率为
位大学生认为“扫黑除恶”与“打黑除恶”不相同的频率为![]()
据此估算该校![]() 名在读大学生中认为“扫黑除恶”与“打黑除恶”不相同的人数为
名在读大学生中认为“扫黑除恶”与“打黑除恶”不相同的人数为![]() .
.
(3)设选取的![]() 位男生和
位男生和![]() 位女生分别记为
位女生分别记为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,随机选取
,随机选取![]() 次采访的所有结果
次采访的所有结果
为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共有10个基本事件,
共有10个基本事件,
至少有一位男生的基本事件有![]() 个,故所求概率为
个,故所求概率为![]()


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某家庭记录了未使用节水龙头50天的日用水量数据(单位:m3)和使用了节水龙头50天的日用水量数据,得到频数分布表如下:
未使用节水龙头50天的日用水量频数分布表
日用 水量 |
|
|
|
|
|
|
|
频数 | 1 | 3 | 2 | 4 | 9 | 26 | 5 |
使用了节水龙头50天的日用水量频数分布表
日用 水量 |
|
|
|
|
|
|
频数 | 1 | 5 | 13 | 10 | 16 | 5 |
(1)在答题卡上作出使用了节水龙头50天的日用水量数据的频率分布直方图:
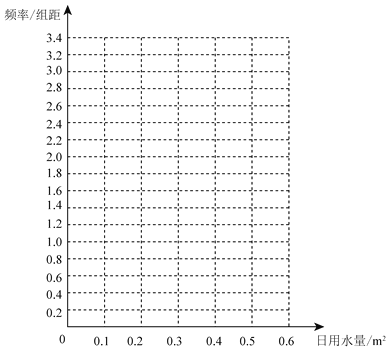
(2)估计该家庭使用节水龙头后,日用水量小于0.35 m3的概率;
(3)估计该家庭使用节水龙头后,一年能节省多少水?(一年按365天计算,同一组中的数据以这组数据所在区间中点的值作代表.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点坐标分别是
的两个焦点坐标分别是![]() 、
、![]() ,并且经过点
,并且经过点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与圆
与圆![]() :
:![]() 相切,并与椭圆
相切,并与椭圆![]() 交于不同的两点
交于不同的两点![]() 、
、![]() .当
.当![]() ,且满足
,且满足![]() 时,求
时,求![]() 面积
面积![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算木》中将底面为长方形,且有一条侧棱与底面垂直的四棱锥称之为“阳马”,现有一阳马,其正视图和侧视图是如图所示的直角三角形,该“阳马”的体积为![]() ,若该阳马的顶点都在同一个球面上,则该球的表面积为( )
,若该阳马的顶点都在同一个球面上,则该球的表面积为( )

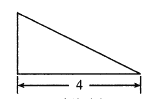
正视图 侧视图
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知极点与直角坐标系原点重合,极轴与x轴的正半轴重合,圆C的极坐标方程为![]() ,直线l的参数方程为
,直线l的参数方程为 为参数
为参数![]() .
.
![]() 若
若![]() ,直线l与x轴的交点为M,N是圆C上一动点,求
,直线l与x轴的交点为M,N是圆C上一动点,求![]() 的最小值;
的最小值;
![]() 若直线l被圆C截得的弦长等于圆C的半径,求a的值.
若直线l被圆C截得的弦长等于圆C的半径,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】规定![]() ,其中
,其中![]() ,
,![]() 是正整数,且
是正整数,且![]() ,这是组合数
,这是组合数![]() (
(![]() 、
、![]() 是正整数,且
是正整数,且![]() )的一种推广.
)的一种推广.
(1)求![]() 的值;
的值;
(2)设![]() ,当
,当![]() 为何值时,
为何值时,![]() 取得最小值?
取得最小值?
(3)组合数的两个性质:①![]() .②
.②![]() .是否都能推广到
.是否都能推广到![]() (
(![]() ,
,![]() 是正整数)的情形?若能推广,则写出推广的形式并给出证明;若不能,则说明理由.
是正整数)的情形?若能推广,则写出推广的形式并给出证明;若不能,则说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市![]() 户居民的月平均用电量(单位:度),以
户居民的月平均用电量(单位:度),以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分组的频率分布直方图如图.
分组的频率分布直方图如图.

(1)求直方图中![]() 的值;
的值;
(2)求月平均用电量的众数和中位数;
(3)在月平均用电量为![]() ,
,![]() ,
,![]() ,
,![]() 的四组用户中,用分层抽样的方法抽取
的四组用户中,用分层抽样的方法抽取![]() 户居民,则月平均用电量在
户居民,则月平均用电量在![]() 的用户中应抽取多少户?
的用户中应抽取多少户?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“克拉茨猜想”又称“![]() 猜想”,是德国数学家洛萨克拉茨在1950年世界数学家大会上公布的一个猜想:任给一个正整数
猜想”,是德国数学家洛萨克拉茨在1950年世界数学家大会上公布的一个猜想:任给一个正整数![]() ,如果
,如果![]() 是偶数,就将它减半;如果
是偶数,就将它减半;如果![]() 为奇数就将它乘3加1,不断重复这样的运算,经过有限步后,最终都能够得到1.己知正整数
为奇数就将它乘3加1,不断重复这样的运算,经过有限步后,最终都能够得到1.己知正整数![]() 经过6次运算后得到1,则
经过6次运算后得到1,则![]() 的值为__________.
的值为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com