
【题目】设函数f(x)=(x2-1)lnx-x2+2x.
(1)求曲线y=f(x)在点(2,f(2))处的切线方程;
(2)证明:f(x)≥1.
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:高中数学 来源: 题型:
【题目】2017年“十一”期间,高速公路车辆较多.某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(![]() )分成六段:
)分成六段: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,后得到如图的频率分布直方图.
,后得到如图的频率分布直方图.

(1)求这40辆小型车辆车速的众数和中位数的估计值;
(2)若从车速在![]() 的车辆中任抽取2辆,求车速在
的车辆中任抽取2辆,求车速在![]() 的车辆恰有一辆的概率.
的车辆恰有一辆的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥P-ABCD中,PC⊥平面ABCD,PC=2,在四边形ABCD中,∠B=∠C=90°,AB=4,CD=1,点M在PB上,PB=4PM,PB与平面ABCD成30°的角.
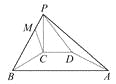
求证:(1)CM∥平面PAD.
(2)平面PAB⊥平面PAD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一辆汽车从A市出发沿海岸一条笔直公路以![]() 的速度向东匀速行驶,汽车开动时,在A市南偏东方向距A市500km且与海岸距离为300km的海上B处有一艘快艇与汽车同时出发,要把一份文件交给这辆汽车的司机.
的速度向东匀速行驶,汽车开动时,在A市南偏东方向距A市500km且与海岸距离为300km的海上B处有一艘快艇与汽车同时出发,要把一份文件交给这辆汽车的司机.
(1)快艇至少以多大的速度行驶才能把文件送到司机手中?
(2)求快艇以最小速度行驶时的行驶方向与![]() 所成角的大小.
所成角的大小.
(3)若快艇每小时最快行驶![]() ,快艇应如何行驶才能尽快把文件交到司机手中?最快需多长时间?
,快艇应如何行驶才能尽快把文件交到司机手中?最快需多长时间?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 定义域为
定义域为![]() ,且对任意实数
,且对任意实数![]() ,有
,有![]() ,则称
,则称![]() 为“
为“![]() 形函数”,若函数
形函数”,若函数![]() 定义域为
定义域为![]() ,函数
,函数![]() 对任意
对任意![]() 恒成立,且对任意实数
恒成立,且对任意实数![]() ,有
,有![]() ,则称为“对数
,则称为“对数![]() 形函数” .
形函数” .
(1)试判断函数![]() 是否为“
是否为“![]() 形函数”,并说明理由;
形函数”,并说明理由;
(2)若![]() 是“对数
是“对数![]() 形函数”,求实数
形函数”,求实数![]() 的取值范围;
的取值范围;
(3)若![]() 是“
是“![]() 形函数”,且满足对任意
形函数”,且满足对任意![]() ,有
,有![]() ,问
,问![]() 是否为“对数
是否为“对数![]() 形函数”?证明你的结论.
形函数”?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区高考实行新方案,规定:语文、数学和英语是考生的必考科目,考生还须从物理、化学、生物、历史、地理和政治六个科目中选取三个科目作为选考科目,若一名学生从六个科目中选出了三个科目作为选考科目,则称该学生的选考方案确定;否则,称该学生选考方案待确定.例如,学生甲选择“物理、化学和生物”三个选考科目,则学生甲的选考方案确定,“物理、化学和生物”为其选考方案.
某学校为了了解高一年级420名学生选考科目的意向,随机选取30名学生进行了一次调查,统计选考科目人数如下表:
性别 | 选考方案确定情况 | 物理 | 化学 | 生物 | 历史 | 地理 | 政治 |
男生 | 选考方案确定的有8人 | 8 | 8 | 4 | 2 | 1 | 1 |
选考方案待确定的有6人 | 4 | 3 | 0 | 1 | 0 | 0 | |
女生 | 选考方案确定的有10人 | 8 | 9 | 6 | 3 | 3 | 1 |
选考方案待确定的有6人 | 5 | 4 | 1 | 0 | 0 | 1 |
(Ⅰ)估计该学校高一年级选考方案确定的学生中选考生物的学生有多少人?
(Ⅱ)假设男生、女生选择选考科目是相互独立的.从选考方案确定的8位男生随机选出1人,从选考方案确定的10位女生中随机选出1人,试求该男生和该女生的选考方案中都含有历史科目的概率;
(Ⅲ)从选考方案确定的8名男生随机选出2名,设随机变量两名男生选考方案相同时![]() ,两名男生选考方案不同时
,两名男生选考方案不同时![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】春节过后,某市教育局从全市高中生中抽去了100人,调查了他们的压岁钱收入情况,按照金额(单位:百元)分成了以下几组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .统计结果如下表所示:
.统计结果如下表所示:
![]()
该市高中生压岁钱收入![]() 可以认为服从正态分布
可以认为服从正态分布![]() ,用样本平均数
,用样本平均数![]() (每组数据取区间的中点值)作为
(每组数据取区间的中点值)作为![]() 的估计值.
的估计值.
(1)求样本平均数![]() ;
;
(2)求![]() ;
;
(3)某文化公司赞助了市教育局的这次社会调查活动,并针对该市的高中生制定了赠送“读书卡”的活动,赠送方式为:压岁钱低于![]() 的获赠两次读书卡,压岁钱不低于
的获赠两次读书卡,压岁钱不低于![]() 的获赠一次读书卡.已知每次赠送的读书卡张数及对应的概率如下表所示:
的获赠一次读书卡.已知每次赠送的读书卡张数及对应的概率如下表所示:

现从该市高中生中随机抽取一人,记![]() (单位:张)为该名高中生获赠的读书卡的张数,求
(单位:张)为该名高中生获赠的读书卡的张数,求![]() 的分布列及数学期望.
的分布列及数学期望.
参考数据:若![]() ,则
,则![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com