

分析 (1)由于抛物线的解析式中只有两个待定系数,因此只需将A、C两点的坐标代入抛物线中即可求出二次函数的解析式;
(2)首先假设出D点坐标,进而表示出S=S△AOD+S△OCD-S△AOC得出答案;
(3)根据抛物线的解析式,可求出B点的坐标,进而能得到直线BC的解析式,设出点P的横坐标,根据直线BC的解析式表示出P点的纵坐标,然后利用坐标系两点间的距离公式分别表示出△ACP三边的长,从而根据:①AP=CP、②AC=AP、③CP=AC,三种不同等量关系求出符合条件的P点坐标.
解答 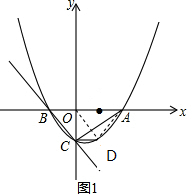 解:(1)由于抛物线经过A(2,0),C(0,-1),
解:(1)由于抛物线经过A(2,0),C(0,-1),
则有c=-1,2+2b+c=0
解得:b=-$\frac{1}{2}$,
故抛物线的解析式为:y=$\frac{1}{2}$x2-$\frac{1}{2}$x-1.
(2)如图1,连接OE,AE
当y=0,则0=x2-x-1,
解得:x1=2,x2=-1,
A(2,0),设D(x,$\frac{1}{2}$x2-$\frac{1}{2}$x-1),
故△ACD的面积:
S=S△AOD+S△OCD-S△AOC
=$\frac{1}{2}$×2×[-($\frac{1}{2}$ x2-$\frac{1}{2}$x-1)+×1×x-$\frac{1}{2}$×1×2
=-$\frac{1}{2}$x2+x
=-(x-1)2+$\frac{1}{2}$,
因此当x=1,
即D(1,-1)时,△ACE的面积最大,且最大值为$\frac{1}{2}$.
(3)由(1)的抛物线解析式易知:B(-1,0),
可求得直线BC的解析式为:y=-x-1;
设P(x,-x-1),因为A(2,0),C(0,-1),则有:
AP2=(x-2)2+(-x-1)2=2x2-2x+5,
AC2=5,CP2=x2+(-x-1+1)2=2x2;
①如图2,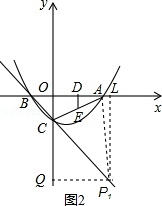
当AP=CP时,AP2=CP2,有:
2x2-2x+5=2x2,解得x=2.5,
故P1(2.5,-3.5);
②如图3,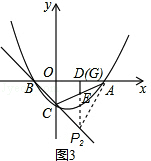
当AP=AC时,AP2=AC2,有:
2x2-2x+5=5,
解得:x=0(舍去),x=1,
故P2(1,-2);
③如图4,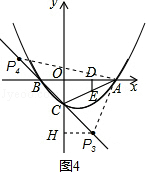
当CP=AC时,CP2=AC2,有:
2x2=5,
解得:x=±$\frac{\sqrt{10}}{2}$,
故P3($\frac{\sqrt{10}}{2}$,-$\frac{\sqrt{10}}{2}$-1),P4(-$\frac{\sqrt{10}}{2}$,$\frac{\sqrt{10}}{2}$-1);
综上所述,存在符合条件的P点,且P点坐标为:P1(2.5,-3.5),P2(1,-2),P3($\frac{\sqrt{10}}{2}$,-$\frac{\sqrt{10}}{2}$-1),P4(-$\frac{\sqrt{10}}{2}$,$\frac{\sqrt{10}}{2}$-1).
点评 此题主要考查了二次函数解析式的确定、图形面积的求法、二次函数最值的应用、等腰三角形的构成条件等重要知识,同时还考查了分类讨论、数形结合的数学思想,属于难题.


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{12}{13}$ | B. | $\frac{5}{13}$ | C. | -$\frac{5}{12}$ | D. | -$\frac{12}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | 5 | D. | $\frac{1}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com