
 ),从而求出X的数学期望;
),从而求出X的数学期望;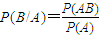 .
.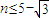 或
或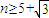 .
.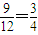 .
.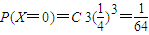 ,
,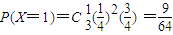 ,
,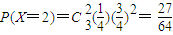 ,
,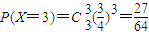 ,
,| X | 0 | 1 | 2 | 3 |
| P | 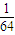 | 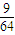 | 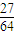 | 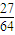 |
 ).所以X的数学期望EX=3×
).所以X的数学期望EX=3× =
= .
.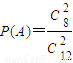 ,
,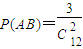 ,
,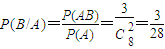 .
.

 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分12分)
箱中装有12张大小、重量一样的卡片,每张卡片正面分别标有1到12中的一个号码,正面号码为![]() 的卡片反面标的数字是
的卡片反面标的数字是![]() .(卡片正反面用颜色区分)
.(卡片正反面用颜色区分)
(Ⅰ)如果任意取出一张卡片,试求正面数字不大于反面数字的概率;
(Ⅱ)如果同时取出两张卡片,试求他们反面数字相同的概率.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省揭阳一中高三(下)第一次测试数学试卷(文科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com