
【题目】设有直线![]() 和平面
和平面![]() ,则下列四个命题中,正确的是( )
,则下列四个命题中,正确的是( )
A. 若m∥α,n∥α,则m∥nB. 若mα,nα,m∥β,l∥β,则α∥β
C. 若α⊥β,mα,则m⊥βD. 若α⊥β,m⊥β,mα,则m∥α
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:
【题目】给出下列说法:①用 刻画回归效果,当
刻画回归效果,当![]() 越大时,模型的拟合效果越差,反之则越好;②归纳推理是由特殊到一般的推理,而演绎推移则是由一般到特殊的推理;③综合法证明数学问题是“由因索果”,分析法证明数学问题是“执果索因”;④设有一个回归方程
越大时,模型的拟合效果越差,反之则越好;②归纳推理是由特殊到一般的推理,而演绎推移则是由一般到特殊的推理;③综合法证明数学问题是“由因索果”,分析法证明数学问题是“执果索因”;④设有一个回归方程![]() ,变量
,变量![]() 增加1个单位时,
增加1个单位时,![]() 平均增加5个单位;⑤线性回归方程
平均增加5个单位;⑤线性回归方程![]() 必过点
必过点![]() .其中错误的个数有( )
.其中错误的个数有( )
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆E: ![]() 的焦点在x轴上
的焦点在x轴上
(1)若椭圆E的焦距为1,求椭圆E的方程;
(2)设F1 , F2分别是椭圆E的左、右焦点,P为椭圆E上第一象限内的点,直线F2P交y轴于点Q,并且F1P⊥F1Q,证明:当a变化时,点P在某定直线上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),过点
),过点![]() 的直线
的直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).
为参数).
(Ⅰ)求曲线![]() 的普通方程,并说明它表示什么曲线;
的普通方程,并说明它表示什么曲线;
(Ⅱ)设曲线![]() 与直线
与直线![]() 分别交于
分别交于![]() ,
,![]() 两点,若
两点,若![]() ,
,![]() ,
,![]() 成等比数列,求
成等比数列,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=alnx+ ![]() +
+ ![]() x+1,其中a∈R,曲线y=f(x)在点(1,f(1))处的切线垂直于y轴.
x+1,其中a∈R,曲线y=f(x)在点(1,f(1))处的切线垂直于y轴.
(1)求a的值;
(2)求函数f(x)的极值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某个命题与正整数n有关,如果当![]() 时命题成立,那么可推得当
时命题成立,那么可推得当![]() 时命题也成立. 现已知当n=8时该命题不成立,那么可推得 ( )
时命题也成立. 现已知当n=8时该命题不成立,那么可推得 ( )
A. 当n=7时该命题不成立 B. 当n=7时该命题成立
C. 当n=9时该命题不成立 D. 当n=9时该命题成立
查看答案和解析>>
科目:高中数学 来源: 题型:
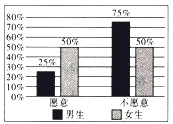
【题目】某组织在某市征集志愿者参加志愿活动,现随机抽出60名男生和40名女生共100人进行调查,统计出100名市民中愿意参加志愿活动和不愿意参加志愿活动的男女生比例情况,具体数据如图所示.
(1)根据条件完成下列![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为愿意参与志愿活动与性别有关?
的把握认为愿意参与志愿活动与性别有关?
愿意 | 不愿意 | 总计 | |
男生 | |||
女生 | |||
总计 |
(2)现用分层抽样的方法从愿意参加志愿活动的市民中选取7名志愿者,再从中抽取2人作为队长,求抽取的2人至少有一名女生的概率.
参考数据及公式:
|
|
|
|
|
|
|
|
|
|
![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com