Question

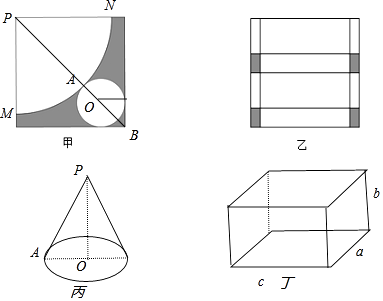
【题目】将2张边长均为1分米的正方形纸片分别按甲、乙两种方式剪裁并废弃阴影部分．

（1）在图甲的方式下，剩余部分恰能完全覆盖某圆锥的表面，求该圆锥的母线长及底面半径；
（2）在图乙的方式下，剩余部分能完全覆盖一个长方体的表面，求长方体体积的最大值．

Answer 1

【答案】
（1）解：甲图对应的圆锥如图丙，圆锥母线为PA=L，圆锥底面圆半径为OA=r

则有L+r+ = ， 解得L= ，r=

∴该圆锥的母线长及底面半径分别为 分米、 分米

（2）解：图乙剩余部分覆盖的长方体如图丁所示，设其棱长为a，b，c

则2（a+b）=1，2b+c=1a= ，c=1﹣2b

长方体体积的V=abc=（ ）b（1﹣2b）= ，（0 ）

令g（b）= ，（0 ），g′（b）=4b2﹣4b+ =（3b﹣ ）（2b﹣1）

b 时，g′（b）＞0，b 时，g′（b）＜0

∴g（b）在（0， ）递增，在（ ）递减，

∴当b= 时，长方体体积最大值，Vmax=（ ）× ×（1﹣2× ）= ．

【解析】（1）设圆锥母线长为L，底面半径为r，则根据题意可知L+r+r=（正方形的对角线长），然后根据扇形弧长=底面圆的周长列出另一个关于L、r的方程，两方程联立即可求解；（2）设长方体棱长分别为a、b、c，然后根据题意将长方体体积V用b表示，构造函数g（b），利用导数讨论g（b）的单调性进而求出V的最大值.
【考点精析】利用旋转体（圆柱、圆锥、圆台）对题目进行判断即可得到答案，需要熟知常见的旋转体有：圆柱、圆锥、圆台、球．