
【题目】两个三口之家,共![]() 个大人,
个大人,![]() 个小孩,约定星期日乘红色、白色两辆轿车结伴郊游,每辆车最多乘坐
个小孩,约定星期日乘红色、白色两辆轿车结伴郊游,每辆车最多乘坐![]() 人,其中两个小孩不能独坐一辆车,则不同的乘车方法种数是_____.
人,其中两个小孩不能独坐一辆车,则不同的乘车方法种数是_____.
【答案】![]()
【解析】
只需确定红色轿车上的乘车人员即可,分七种情况讨论:![]() 个小孩
个小孩![]() 个大人,
个大人,![]() 个小孩
个小孩![]() 个大人,
个大人,![]() 个小孩
个小孩![]() 个大人,
个大人,![]() 个小孩
个小孩![]() 个大人,
个大人,![]() 个小孩
个小孩![]() 个大人,
个大人,![]() 个大人、
个大人、![]() 个大人,利用分类计算原理可得出结果.
个大人,利用分类计算原理可得出结果.
根据题意,只需确定红色轿车上的乘车人员即可,其他人乘坐白色轿车,
由于每辆车最多乘坐![]() 人,其中两个小孩不能独坐一辆车,分以下七种情况讨论:
人,其中两个小孩不能独坐一辆车,分以下七种情况讨论:
①红色轿车中有![]() 个小孩
个小孩![]() 个大人,有
个大人,有![]() 种安排方法;
种安排方法;
②红色轿车中有![]() 个小孩
个小孩![]() 个大人,有
个大人,有![]() 种安排方法;
种安排方法;
③红色轿车中有![]() 个小孩
个小孩![]() 个大人,有
个大人,有![]() 种安排方法;
种安排方法;
④红色轿车中有![]() 个小孩
个小孩![]() 个大人,有
个大人,有![]() 种安排方法;
种安排方法;
⑤红色轿车中有![]() 个小孩
个小孩![]() 个大人,有
个大人,有![]() 种安排方法;
种安排方法;
⑥红色轿车中有![]() 个大人,有
个大人,有![]() 种安排方法;
种安排方法;
⑦红色轿车中有![]() 个大人,有
个大人,有![]() 种安排方法.
种安排方法.
综上所述,共有![]() 种安排方法.
种安排方法.
故答案为:![]() .
.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() (
(![]() ),过原点的两条直线
),过原点的两条直线![]() 和
和![]() 分别与
分别与![]() 交于点
交于点![]() 、
、![]() 和
和![]() 、
、![]() ,得到平行四边形
,得到平行四边形![]() .
.
(1)若![]() ,
,![]() ,且
,且![]() 为正方形,求该正方形的面积
为正方形,求该正方形的面积![]() .
.
(2)若直线![]() 的方程为
的方程为![]() ,
,![]() 和
和![]() 关于
关于![]() 轴对称,
轴对称,![]() 上任意一点
上任意一点![]() 到
到![]() 和
和![]() 的距离分别为
的距离分别为![]() 和
和![]() ,证明:
,证明:![]() .
.
(3)当![]() 为菱形,且圆
为菱形,且圆![]() 内切于菱形
内切于菱形![]() 时,求
时,求![]() ,
,![]() 满足的关系式.
满足的关系式.
查看答案和解析>>
科目:高中数学 来源: 题型:
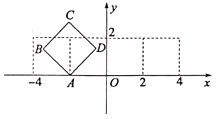
【题目】在平面直角坐标系![]() 中,如图放置的边长为
中,如图放置的边长为![]() 的正方形
的正方形![]() 沿
沿![]() 轴滚动(无滑动滚动),点
轴滚动(无滑动滚动),点![]() 恰好经过坐标原点,设顶点
恰好经过坐标原点,设顶点![]() 的轨迹方程是
的轨迹方程是![]() ,则对函数
,则对函数![]() 的判断正确的是( )
的判断正确的是( )
A.函数![]() 是奇函数B.对任意的
是奇函数B.对任意的![]() ,都有
,都有![]()
C.函数![]() 的值域为
的值域为![]() D.函数
D.函数![]() 在区间
在区间![]() 上单调递增
上单调递增
查看答案和解析>>
科目:高中数学 来源: 题型:
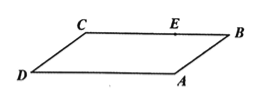
【题目】如图,有一块平行四边形绿地![]() ,经测量
,经测量![]() 百米,
百米,![]() 百米,
百米,![]() ,拟过线段
,拟过线段![]() 上一点
上一点![]() 设计一条直路
设计一条直路![]() (点
(点![]() 在四边形
在四边形![]() 的边上,不计路的宽度),
的边上,不计路的宽度),![]() 将绿地分成两部分,且右边面积是左边面积的3倍,设
将绿地分成两部分,且右边面积是左边面积的3倍,设![]() 百米,
百米,![]() 百米.
百米.
(1)当点![]() 与点
与点![]() 重合时,试确定点
重合时,试确定点![]() 的位置;
的位置;
(2)试求![]() 的值,使路
的值,使路![]() 的长度
的长度![]() 最短.
最短.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某人打算做一个正四棱锥形的金字塔模型,先用木料搭边框,再用其他材料填充,已知金字塔的每一条棱和边都相等.
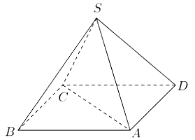
(1)求证:直线AC垂直于直线SD;
(2)若搭边框共使用木料24米,则需要多少立方米的填充材料才能将整个金字塔内部填满?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列![]() 满足
满足![]() .
.
①存在![]() 可以生成的数列
可以生成的数列![]() 是常数数列;
是常数数列;
②“数列![]() 中存在某一项
中存在某一项![]() ”是“数列
”是“数列![]() 为有穷数列”的充要条件;
为有穷数列”的充要条件;
③若![]() 为单调递增数列,则
为单调递增数列,则![]() 的取值范围是
的取值范围是![]() ;
;
④只要![]() ,其中
,其中![]() ,则
,则![]() 一定存在;
一定存在;
其中正确命题的序号为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 中,
中,![]() ,
,![]() ,
,![]() 的前
的前![]() 项和为
项和为![]() ,且满足
,且满足![]() (
(![]() ).
).
(1)试求数列![]() 的通项公式;
的通项公式;
(2)令![]() ,
,![]() 是
是![]() 的前
的前![]() 项和,证明:
项和,证明:![]() ;
;
(3)证明:对任意给定的![]() ,均存在
,均存在![]() ,使得
,使得![]() 时,(2)中的
时,(2)中的![]() 恒成立.
恒成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列 ![]() 的前
的前![]() 项和为
项和为![]() ,对一切
,对一切![]() ,点
,点![]() 都在函数
都在函数![]() 的图象上.
的图象上.
(1)求![]() ,归纳数列
,归纳数列![]() 的通项公式(不必证明);
的通项公式(不必证明);
(2)将数列![]() 依次按1项、2项、3项、4项循环地分为
依次按1项、2项、3项、4项循环地分为![]() ,
,![]() ,
,![]() ,
, ![]() ;
;![]() ,
,![]() ,
,![]() ,
,![]() ;
;![]() ,…,分别计算各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列为
,…,分别计算各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列为![]() ,求
,求![]() 的值;
的值;
(3)设![]() 为数列
为数列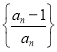 的前
的前![]() 项积,若不等式
项积,若不等式![]() 对一切
对一切![]() 都成立,其中
都成立,其中![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com