
【题目】调查某校 100 名学生的数学成绩情况,得下表:
一般 | 良好 | 优秀 | |
男生(人) |
| 18 |
|
女生(人) | 10 | 17 |
|
已知从这批学生中随机抽取1名学生,抽到成绩一般的男生的概率为0.15.
(1)求![]() 的值;
的值;
(2)若用分层抽样的方法,从这批学生中随机抽取20名,问应在优秀学生中抽多少名?
(3)已知![]() ,优秀学生中男生不少于女生的概率.
,优秀学生中男生不少于女生的概率.
【答案】(1)15人;(2)8名;(3)![]() .
.
【解析】试题分析:(1)由于抽到成绩一般的男生的概率为0.15,可得![]() ,由此解得 x的值;
,由此解得 x的值;
(2)先求出每个个体被抽到的概率,优秀的学生人数y+z 的值,用所求得的概率乘以(y+z)的值,即可得应抽取的优秀学生人数;
(3)由于y+z=40,y≥17,z≥18,用列举法求得所有的(y,z)有6个,而满足条件的(y,z)有3个,由此求得所求事件的概率.
试题解析:
(1)由题意可知, ![]() ∴
∴![]() (人)
(人)
(2)由题意可知,优秀人数为![]() (人)
(人)
设应在优秀中抽取![]() 人,则
人,则
![]() ,∴
,∴![]() (人)
(人)
所以应在优秀中抽 8 名
(3)由题意可知, ![]() ,且
,且![]() ,满足条件的
,满足条件的![]() 有
有![]() ,
, ![]() ,共有6组.
,共有6组.
设事件![]() 为“优秀学生中男生不少于女生”,即
为“优秀学生中男生不少于女生”,即![]() ,满足条件的
,满足条件的![]() 有
有![]() ,
, ![]() 共有3组,所以
共有3组,所以
![]() .即优秀学生中女生少于男生的概率为
.即优秀学生中女生少于男生的概率为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数![]() ,且
,且![]() 在
在![]() 和
和![]() 处取得极值.
处取得极值.
(1)求函数![]() 的解析式;
的解析式;
(2)设函数![]() ,是否存在实数
,是否存在实数![]() ,使得曲线
,使得曲线![]() 与
与![]() 轴有两个交点,若存在,求出
轴有两个交点,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小区规划时,计划在周边建造一片扇形绿地,如图所示已知扇形绿地的半径为50米,圆心角![]() 从绿地的圆弧边界上不同于A,B的一点P处出发铺设两条道路PO与
从绿地的圆弧边界上不同于A,B的一点P处出发铺设两条道路PO与![]() 均为直线段
均为直线段![]() ,其中PC平行于绿地的边界
,其中PC平行于绿地的边界![]() 记
记![]() 其中
其中![]()
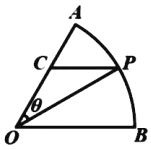
![]() 当
当![]() 时,求所需铺设的道路长:
时,求所需铺设的道路长:
![]() 若规划中,绿地边界的OC段也需铺设道路,且道路的铺设费用均为每米100元,当
若规划中,绿地边界的OC段也需铺设道路,且道路的铺设费用均为每米100元,当![]() 变化时,求铺路所需费用的最大值
变化时,求铺路所需费用的最大值![]() 精确到1元
精确到1元![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商品要了解年广告费![]() (单位:万元)对年销售额
(单位:万元)对年销售额![]() (单位:万元)的影响,对近4年的年广告费
(单位:万元)的影响,对近4年的年广告费![]() 和年销售额
和年销售额![]() 数据作了初步整理,得到下面的表格:
数据作了初步整理,得到下面的表格:

用广告费作解释变量,年销售额作预报变量,若认为![]() 适宜作为年销售额
适宜作为年销售额![]() 关于年广告费
关于年广告费![]() 的回归方程类型,则
的回归方程类型,则
(1)根据表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)已知商品的年利润![]() 与
与![]() 的关系式为
的关系式为![]() .根据(1)的结果,年广告费
.根据(1)的结果,年广告费![]() 约为何值时(小数点后保留两位),年利润的预报值最大?
约为何值时(小数点后保留两位),年利润的预报值最大?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为
 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2ax2+bx+1(e为自然对数的底数).
(1)若 ![]() ,求函数F(x)=f(x)ex的单调区间;
,求函数F(x)=f(x)ex的单调区间;
(2)若b=e﹣1﹣2a,方程f(x)=ex在(0,1)内有解,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】能被3整除,且构成每个数的数码只限于1、2、3(1、2、3可以不全部用到)的所有小于200000的不同自然数个数是_____________________。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|a﹣3x|﹣|2+x|.
(1)若a=2,解不等式f(x)≤3;
(2)若存在实数a,使得不等式f(x)≥1﹣a+2|2+x|成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 分别是正方体
分别是正方体![]() 的棱
的棱![]() 上两点,且
上两点,且![]() ,给出下列四个命题:①三棱锥
,给出下列四个命题:①三棱锥![]() 的体积为定值;②异面直线
的体积为定值;②异面直线![]() 与
与![]() 所成的角为
所成的角为![]() ;③
;③![]() 平面
平面![]() ;④直线
;④直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() .其中正确的命题为( )
.其中正确的命题为( )
A. ①② B. ②③ C. ①②④ D. ①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某服装厂生产一种服装,每件服装成本为40元,出厂单价定为60元,该厂为鼓励销售商订购,规定当一次订购量超过100件时,每多订购一件,订购的全部服装的出厂单价就降低![]() 元,根据市场调查,销售商一次订购不会超过600件.
元,根据市场调查,销售商一次订购不会超过600件.
(1)设一次订购![]() 件,服装的实际出厂单价为
件,服装的实际出厂单价为![]() 元,写出函数
元,写出函数![]() 的表达式;
的表达式;
(2)当销售商一次订购多少件服装时,该厂获得的利润最大?其最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com