
【题目】用0与1两个数字随机填入如图所示的5个格子里,每个格子填一个数字,并且从左到右数,不管数到哪个格子,总是1的个数不少于0的个数,则这样填法的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
由题意列出所有可能的结果,然后利用古典概型计算公式确定满足题意的概率值即可.
由题意可知,填写的可能结果共有如下32种:
00000,00001,00010,00011,00100,00101,00110,00111,
01000,01001,01010,01011,01100,01101,01110,01111,
10000,10001,10010,10011,10100,10101,10110,10111,
11000,11001,11010,11011,11100,11101,11110,11111,
其中满足题意的有10种:
10101,10110,10111,11001,11010,11011,11100,11101,11110,11111,
由古典概型计算公式可得满足题意的概率值为:![]() .
.
本题选择B选项.


科目:高中数学 来源: 题型:
【题目】已知y=f(x)是定义在(-∞,+∞)上的奇函数,且在[0,+∞)上为增函数,
(1)求证:函数在(-∞,0)上也是增函数;
(2)如果f(![]() )=1,解不等式-1<f(2x+1)≤0.
)=1,解不等式-1<f(2x+1)≤0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在党中央的正确指导下,通过全国人民的齐心协力,特别是全体一线医护人员的奋力救治,二月份“新冠肺炎”疫情得到了控制.下图是国家卫健委给出的全国疫情通报,甲、乙两个省份从2月7日到2月13日一周的新增“新冠肺炎”确诊人数的折线图如下:
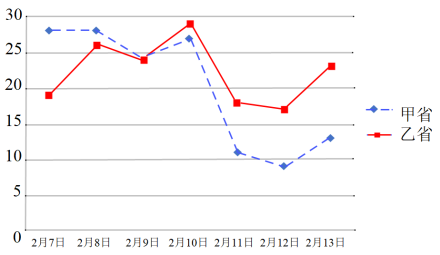
根据图中甲、乙两省的数字特征进行比对,通过比较把你得到最重要的两个结论写在答案纸指定的空白处.
①_________________________________________________.
②_________________________________________________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}中,a1=2,n(an+1﹣an)=an+1,n∈N*.
(1)设bn =![]() ,求数列{bn}的通项公式;
,求数列{bn}的通项公式;
(2)若对于任意的t∈[0,1],n∈N*,不等式![]() 2t2﹣(a+1)t+a2﹣a+3恒成立,求实数a的取值范围.
2t2﹣(a+1)t+a2﹣a+3恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙3位大学生同时应聘某个用人单位的职位,甲、乙两人只有一人被选中的概率为![]() ,两人都被选中的概率为
,两人都被选中的概率为![]() ,丙被选中的概率为
,丙被选中的概率为![]() ,且三人各自能否被选中互不影响.
,且三人各自能否被选中互不影响.
(1)求3人同时被选中的概率;
(2)求恰好有2人被选中的概率;
(3)求3人中至少有1人被选中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 和
和![]() 满足
满足![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)证明:![]() 是等比数列,
是等比数列,![]() 是等差数列;
是等差数列;
(2)求![]() 和
和![]() 的通项公式;
的通项公式;
(3)令 ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() 的通项公式,并求数列
的通项公式,并求数列![]() 的最大值、最小值,并指出分别是第几项.
的最大值、最小值,并指出分别是第几项.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我们国家正处于老龄化社会中,老有所依也是政府的民生工程.某市共有户籍人口400万,其中老人(年龄60岁及以上)人数约有66万,为了了解老人们的健康状况,政府从老人中随机抽取600人并委托医疗机构免费为他们进行健康评估,健康状况共分为不能自理、不健康尚能自理、基本健康、健康四个等级,并以80岁为界限分成两个群体进行统计,样本分布被制作成如下图表:
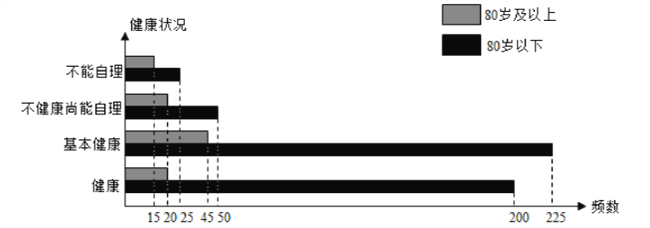
(1)若采用分层抽样的方法再从样本中的不能自理的老人中抽取8人进一步了解他们的生活状况,则两个群体中各应抽取多少人?
(2)估算该市80岁及以上长者占全市户籍人口的百分比;
(3)据统计该市大约有五分之一的户籍老人无固定收入,政府计划为这部分老人每月发放生活补贴,标准如下:
①80岁及以上长者每人每月发放生活补贴200元;
②80岁以下老人每人每月发放生活补贴120元;
③不能自理的老人每人每月额外发放生活补贴100元.
利用样本估计总体,试估计政府执行此计划的年度预算.(单位:亿元,结果保留两位小数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2010-2018年之间,受益于基础设施建设对光纤产品的需求,以及个人计算机及智能手机的下一代规格升级,电动汽车及物联网等新机遇,连接器行业增长呈现加速状态.根据该折线图,下列结论正确的个数为( )

①每年市场规模量逐年增加;
②增长最快的一年为2013~2014;
③这8年的增长率约为40%;
④2014年至2018年每年的市场规模相对于2010年至2014年每年的市场规模,数据方差更小,变化比较平稳
A. 1B. 2C. 3D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com