
°æƒø°ø÷∏flπ˝Ω≠¥Û«≈µƒ≥µ¡æÕ®––ƒ‹¡¶ø…∏ƒ…∆’˚∏ˆ≥« –µƒΩªÕ®◊¥øˆ£Æ‘⁄“ª∞„«Èøˆœ¬£¨¥Û«≈…œµƒ≥µ¡˜ÀŸ∂»v£®µ•Œª£∫«ß√◊/–° ±£© «≥µ¡˜√‹∂»x£®µ•Œª£∫¡æ/«ß√◊£©µƒ∫Ø ˝£Æµ±«≈…œµƒ≥µ¡˜√‹∂»¥ÔµΩ200¡æ/«ß√◊ ±£¨‘Ï≥…∂¬»˚£¨¥À ±≥µ¡˜ÀŸ∂»Œ™0£ªµ±≥µ¡˜√‹∂»≤ª≥¨π˝20¡æ/«ß√◊ ±£¨≥µ¡˜ÀŸ∂»Œ™60«ß√◊/–° ±£Æ—–æø±Ì√˜£∫µ±![]() ±£¨≥µ¡˜ÀŸ∂»
±£¨≥µ¡˜ÀŸ∂»![]() «≥µ¡˜√‹∂»
«≥µ¡˜√‹∂»![]() µƒ“ª¥Œ∫Ø ˝£Æ
µƒ“ª¥Œ∫Ø ˝£Æ
£®1£©µ±![]() ±£¨«Û∫Ø ˝
±£¨«Û∫Ø ˝![]() µƒ±Ì¥Ô Ω£ª
µƒ±Ì¥Ô Ω£ª
£®2£©µ±≥µ¡˜√‹∂»![]() Œ™∂‡¥Û ±£¨≥µ¡˜¡ø£®µ•Œª ±º‰ƒ⁄Õ®π˝«≈…œƒ≥π€≤‚µ„µƒ≥µ¡æ ˝£¨µ•Œª£∫¡æ/–° ±£©
Œ™∂‡¥Û ±£¨≥µ¡˜¡ø£®µ•Œª ±º‰ƒ⁄Õ®π˝«≈…œƒ≥π€≤‚µ„µƒ≥µ¡æ ˝£¨µ•Œª£∫¡æ/–° ±£©![]() ø…“‘¥ÔµΩ◊Ó¥Û£¨≤¢«Û≥ˆ◊Ó¥Û÷µ£Æ£®æ´»∑µΩ1¡æ/–° ±£©
ø…“‘¥ÔµΩ◊Ó¥Û£¨≤¢«Û≥ˆ◊Ó¥Û÷µ£Æ£®æ´»∑µΩ1¡æ/–° ±£©
°æ¥∞∏°ø£®1£©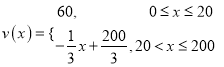 £ª
£ª
£®2£©µ±≥µ¡˜√‹∂»Œ™![]() ¡æ/«ß√◊ ±£¨≥µ¡˜¡ø¥ÔµΩ◊Ó¥Û£¨«“◊Ó¥Û÷µ‘º
¡æ/«ß√◊ ±£¨≥µ¡˜¡ø¥ÔµΩ◊Ó¥Û£¨«“◊Ó¥Û÷µ‘º![]() ¡æ/–° ±.
¡æ/–° ±.
°æΩ‚Œˆ°ø ‘Â∑÷Œˆ£∫£®1£©…Ëv£®x£©=ax+b.¿˚”√xµƒ∑∂Œß£¨¡–≥ˆ∑Ω≥Ã◊È«ÛΩ‚a£¨b£¨º¥ø…µ√µΩ∫Ø ˝µƒΩ‚Œˆ Ω£ª£®2£©«Û≥ˆ≥µ¡˜¡øf£®x£©=v£®x£©xµƒ±Ì¥Ô Ω£¨»ª∫Û«ÛΩ‚◊Ó¥Û÷µº¥ø…
‘Ã‚Ω‚Œˆ£∫£®1£©”…“‚£∫µ±0°‹x°‹20 ±£¨v£®x£©£Ω60£ª
µ±20°‹x°‹200 ±£¨…Ëv£®x£©£Ωax£´b£¨
‘Ÿ”…“—÷™µ√![]() Ω‚µ√
Ω‚µ√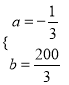 π ∫Ø ˝v£®x£©µƒ±Ì¥Ô ΩŒ™
π ∫Ø ˝v£®x£©µƒ±Ì¥Ô ΩŒ™
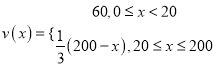
£®2£©“¿Ã‚“‚≤¢”…£®1£©ø…µ√
f£®x£©£Ω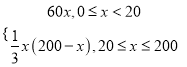
µ±0°‹x°‹20 ±£¨f£®x£©Œ™‘ˆ∫Ø ˝£¨π µ±x£Ω20 ±£¨∆‰◊Ó¥Û÷µŒ™60°¡20£Ω1200£ª
µ±20°‹x°‹200 ±£¨f£®x£©£Ω![]() x£®200£≠x£©°‹
x£®200£≠x£©°‹![]() [
[![]() ]2£Ω
]2£Ω![]() £¨
£¨
µ±«“Ωˆµ±x£Ω200£≠x£¨º¥x£Ω100 ±£¨µ»∫≈≥…¡¢.
À˘“‘£¨µ±x£Ω100 ±£¨f£®x£©‘⁄«¯º‰…œ»°µ√◊Ó¥Û÷µ![]() .
.
◊€…œ£¨µ±x£Ω100 ±£¨f£®x£©‘⁄«¯º‰…œ»°µ√◊Ó¥Û÷µ![]() °÷3 333£¨
°÷3 333£¨
º¥µ±≥µ¡˜√‹∂»Œ™100¡æ/«ß√◊ ±£¨≥µ¡˜¡øø…“‘¥ÔµΩ◊Ó¥Û£¨◊Ó¥Û÷µ‘ºŒ™3 333¡æ/–° ±.


 Õ®≥«—ßµ‰ƒ¨–¥ƒ‹ ÷œµ¡–¥∞∏
Õ®≥«—ßµ‰ƒ¨–¥ƒ‹ ÷œµ¡–¥∞∏
| ƒÍº∂ | ∏fl÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏fl“ª | ∏fl“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏fl∂˛ | ∏fl∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏fl»˝ | ∏fl»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫∏fl÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∫Ø ˝f£®x£©= ![]() x3©Å
x3©Å ![]() £®a° R£©£Æ
£®a° R£©£Æ
£®1£©»Ùa=1£¨«Û∫Ø ˝f£®x£©‘⁄[0£¨2]…œµƒ◊Ó¥Û÷µ£ª
£®2£©»Ù∂‘»Œ“‚x° £®0£¨+°fi£©£¨”–f£®x£©£æ0∫„≥…¡¢£¨«Ûaµƒ»°÷µ∑∂Œß£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏fl÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øµÁ ”¥´√Ωπ´À挙¡ÀΩ‚ƒ≥µÿ«¯µÁ ”π€÷⁄∂‘¿Ô‘º∞¬‘Àª·µƒ ’ ”«Èøˆ£¨Àʪ˙≥È»°¡À100√˚π€÷⁄Ω¯––µ˜≤È£¨∆‰÷–≈Æ–‘”–55√˚£¨œ¬√Ê «∏˘æ›µ˜≤ÈΩ·π˚ªÊ÷∆µƒπ€÷⁄»’æ˘ ’ø¥∏√Ô˝Ω⁄ƒø ±º‰µƒ∆µ¬ ∑÷≤º÷±∑ΩÕº£∫
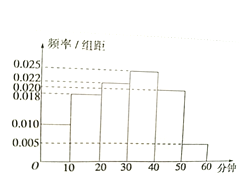
Ω´»’æ˘ ’ø¥∏√Ô˝Ω⁄ƒø ±º‰≤ªµÕ”⁄40∑÷÷”µƒπ€÷⁄≥∆Œ™°∞Ô˝√‘°±°£“—÷™°∞Ô˝√‘°±÷–”–10√˚≈Æ–‘°£
£®1£© ‘«Û°∞Ô˝√‘°±÷–µƒƒ––‘π€÷⁄»À ˝£ª
£®2£©æ›¥À◊ ¡œÕÍ≥…![]() ¡–¡™±Ì£¨ƒ„ «∑Ò»œŒ™°∞Ô˝√‘°±”Ζ‘±”–πÿ£ø
¡–¡™±Ì£¨ƒ„ «∑Ò»œŒ™°∞Ô˝√‘°±”Ζ‘±”–πÿ£ø
∑«Ã”˝√‘ | Ô˝√‘ | ∫œº∆ | |
ƒ– | |||
Ů | |||
∫œº∆ |
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
¡ŸΩÁ÷µ±Ìπ©≤Œøº≤Œøºπ´ Ω£∫
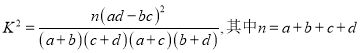
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏fl÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™c>0£¨√¸Ã‚p£∫∫Ø ˝![]() ‘⁄R…œµ•µ˜µ›ºı£¨√¸Ã‚q£∫≤ªµ» Ω
‘⁄R…œµ•µ˜µ›ºı£¨√¸Ã‚q£∫≤ªµ» Ω![]() µƒΩ‚ºØ «R£¨»Ù
µƒΩ‚ºØ «R£¨»Ù![]() Œ™’Ê√¸Ã‚£¨
Œ™’Ê√¸Ã‚£¨ ![]() Œ™ºŸ√¸Ã‚£¨«Ûcµƒ»°÷µ∑∂Œß°£
Œ™ºŸ√¸Ã‚£¨«Ûcµƒ»°÷µ∑∂Œß°£
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏fl÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø…Ëa£æ0£¨ ![]() «R…œµƒ≈º∫Ø ˝£Æ
«R…œµƒ≈º∫Ø ˝£Æ
£®1£©«Ûaµƒ÷µ£ª
£®2£©÷§√˜f£®x£©‘⁄£®0£¨+°fi£©…œŒ™‘ˆ∫Ø ˝£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏fl÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄µ◊√ÊŒ™æÿ–ŒµƒÀƒ¿‚◊∂![]() ÷–£¨
÷–£¨ ![]() .
.
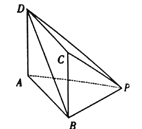
£®1£©÷§√˜£∫∆Ω√Ê![]() ∆Ω√Ê
∆Ω√Ê![]() £ª
£ª
£®2£©»Ù“Ï√Ê÷±œfl![]() ”Î
”Î![]() À˘≥…Ω«Œ™
À˘≥…Ω«Œ™![]() £¨
£¨ ![]() £¨
£¨ ![]() £¨«Û∂˛√ÊΩ«
£¨«Û∂˛√ÊΩ«![]() µƒ¥Û–°.
µƒ¥Û–°.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏fl÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÙÕ÷‘≤C1£∫ ![]() µƒ¿Î–ƒ¬ µ»”⁄
µƒ¿Î–ƒ¬ µ»”⁄ ![]() £¨≈◊ŒÔœflC2£∫x2=2py£®p£æ0£©µƒΩ𵄑⁄Õ÷‘≤C1µƒ∂•µ„…œ£Æ
£¨≈◊ŒÔœflC2£∫x2=2py£®p£æ0£©µƒΩ𵄑⁄Õ÷‘≤C1µƒ∂•µ„…œ£Æ
£®1£©«Û≈◊ŒÔœflC2µƒ∑Ω≥ãª
£®2£©«Ûπ˝µ„M£®©Å1£¨0£©µƒ÷±œfll”Î≈◊ŒÔœflC2ΩªE°¢F¡Ωµ„£¨”÷π˝E°¢F◊˜≈◊ŒÔœflC2µƒ«–œfll1°¢l2 £¨ µ±l1°Õl2 ±£¨«Û÷±œfllµƒ∑Ω≥ãÆ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏fl÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø∂‘”⁄»˝¥Œ∫Ø ˝f£®x£©=ax3+bx2+cx+d£®a°Ÿ0£©£¨∏¯≥ˆ∂®“£∫…Ëf°‰£®x£© «∫Ø ˝y=f£®x£©µƒµº ˝£¨f°‰°‰£®x£© «f°‰£®x£©µƒµº ˝£¨»Ù∑Ω≥Ãf°‰°‰£®x£©”– µ ˝Ω‚x0 £¨ ‘Ú≥∆µ„£®x0 £¨ f£®x0£©£©Œ™∫Ø ˝y=f£®x£©µƒ°∞𒵄°±£Æƒ≥Õ¨—ßæ≠π˝ÃΩæø∑¢œ÷£∫»Œ∫Œ“ª∏ˆ»˝¥Œ∫Ø ˝∂º”–°∞𒵄°±£ª»Œ∫Œ“ª∏ˆ»˝¥Œ∫Ø ˝∂º”–∂‘≥∆÷––ƒ£¨«“°∞𒵄°±æÕ «∂‘≥∆÷––ƒ£Æ…Ë∫Ø ˝f£®x£©= ![]() x3©Å
x3©Å ![]() x2+3x©Å
x2+3x©Å ![]() £¨«Îƒ„∏˘æ›’‚“ª∑¢œ÷£¨º∆À„f£®
£¨«Îƒ„∏˘æ›’‚“ª∑¢œ÷£¨º∆À„f£® ![]() £©+f£®
£©+f£® ![]() £©+f£®
£©+f£® ![]() £©+°≠+f£®
£©+°≠+f£® ![]() £©= £Æ
£©= £Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏fl÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∫Ø ˝f£®x£©=log4£®4x+1£©©Å ![]() x£Æ
x£Æ
£®1£© ‘≈–∂œ∫Ø ˝f£®x£©µƒ∆Ê≈º–‘≤¢÷§√˜£ª
£®2£©…Ëg£®x£©=log4£®a2x©Å ![]() a£©£¨»Ù∫Ø ˝f£®x£©”Îg£®x£©µƒÕºœÛ”–«“÷ª”–“ª∏ˆπ´π≤µ„£¨«Û µ ˝aµƒ»°÷µ∑∂Œß£Æ
a£©£¨»Ù∫Ø ˝f£®x£©”Îg£®x£©µƒÕºœÛ”–«“÷ª”–“ª∏ˆπ´π≤µ„£¨«Û µ ˝aµƒ»°÷µ∑∂Œß£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒfi÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com