
【题目】在四棱锥![]() 中,
中,![]() 平面
平面![]() ,正方形
,正方形![]() 的边长为2,
的边长为2,![]() ,设
,设![]() 为侧棱
为侧棱![]() 的中点.
的中点.
(1)求正四棱锥![]() 的体积
的体积![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角
所成角![]() 的大小.
的大小.
科目:高中数学 来源: 题型:
【题目】《九章算术》卷五《商功》中有如下叙述“今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高一丈“刍甍”指的是底面为矩形的对称型屋脊状的几何体,“下广三丈”是指底面矩形宽三丈,“袤四丈”是指底面矩形长四丈,“上袤二丈”是指脊长二丈,“无宽”是指脊无宽度,“高一丈”是指几何体的高为一丈.现有一个刍甍如图所示,下广三丈,袤四丈,上袤三丈,无广,高二丈,则该刍甍的外接球的表面积为_______________平方丈.
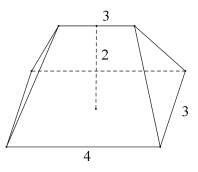
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设一组数据的平均数是2.8,方差是3.6,若将这组数据中的每一个数据都加上10,得到一组新数据,则所得新数据的平均数和方差分别是( )
A.12.8 3.6 B.2.8 13.6 C.12.8 13.6 D.13.6 12.8
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校学生会为研究该校学生的性别与语文、数学、英语成绩这3个变量之间的关系,随机抽查了100名学生,得到某次期末考试的成绩数据如表1至表3,根据表中数据可知该校学生语文、数学、英语这三门学科中( )
表1 | 表2 | 表3 | |||||||||||||
语文 性别 | 不及格 | 及格 | 总计 | 数学 性别 | 不及格 | 及格 | 总计 | 英语 性别 | 不及格 | 及格 | 总计 | ||||
男 | 14 | 36 | 50 | 男 | 10 | 40 | 50 | 男 | 25 | 25 | 50 | ||||
女 | 16 | 34 | 50 | 女 | 20 | 30 | 50 | 女 | 5 | 45 | 50 | ||||
总计 | 30 | 70 | 100 | 总计 | 30 | 70 | 100 | 总计 | 30 | 70 | 100 | ||||
A.语文成绩与性别有关联性的可能性最大,数学成绩与性别有关联性的可能性最小
B.数学成绩与性别有关联性的可能性最大,语文成绩与性别有关联性的可能性最小
C.英语成绩与性别有关联性的可能性最大,语文成绩与性别有关联性的可能性最小
D.英语成绩与性别有关联性的可能性最大,数学成绩与性别有关联性的可能性最小
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某污水处理厂要在一个矩形污水处理池(ABCD)的池底水平铺设污水净化管道(管道构成Rt△FHE,H是直角项点)来处理污水.管道越长,污水净化效果越好.设计要求管道的接口H是AB的中点,E,F分别落在线段BC,AD上.已知AB=20米,AD=![]() 米,记∠BHE=
米,记∠BHE=![]() .
.

(1)试将污水净化管道的长度L表示为![]() 的函数,并写出定义域;
的函数,并写出定义域;
(2)当![]() 取何值时,污水净化效果最好?并求出此时管道的长度L.
取何值时,污水净化效果最好?并求出此时管道的长度L.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 是圆柱的直径,
是圆柱的直径,![]() 是圆柱的母线,
是圆柱的母线,![]() ,
,![]() ,点
,点![]() 是圆柱底面圆周上的点.
是圆柱底面圆周上的点.
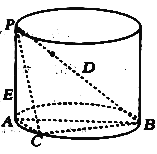
(1)求三棱锥![]() 体积的最大值;
体积的最大值;
(2)若![]() ,
,![]() 是线段
是线段![]() 上靠近点
上靠近点![]() 的三等分点,点
的三等分点,点![]() 是线段
是线段![]() 上的动点,求
上的动点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,AB//CD,且![]()

(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC, ![]() ,且四棱锥P-ABCD的体积为
,且四棱锥P-ABCD的体积为![]() ,求该四棱锥的侧面积.
,求该四棱锥的侧面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com