
【题目】![]() 设函数f(x)=emx+x2-mx
设函数f(x)=emx+x2-mx
(1)(I)证明:f(x)在(-![]() ,0)单调递减,在(0,+
,0)单调递减,在(0,+![]() )单调递增;
)单调递增;
(2)(II)若对于任意x1 , x2![]() [-1,1],都有|f(x1)-f(x2)|
[-1,1],都有|f(x1)-f(x2)|![]() e-1,求m的取值范围。
e-1,求m的取值范围。
【答案】
(1)
证明:(I)f‘(x)=m(emx-1)+2x
若m![]() 0,则当x
0,则当x![]() (-
(-![]() ,0)时,emx-1
,0)时,emx-1![]() 0,f‘(x)
0,f‘(x)![]() 0;当x
0;当x![]() (0,+
(0,+![]() )时,emx-1
)时,emx-1![]() 0,f‘(x)
0,f‘(x)![]() 0.
0.
若m![]() 0,则当x
0,则当x![]() (-
(-![]() ,0)时,emx-1
,0)时,emx-1![]() 0,f‘(x)
0,f‘(x)![]() 0’;当当x
0’;当当x![]() (0,+
(0,+![]() )时,emx-1
)时,emx-1![]() 0,f‘(x)
0,f‘(x)![]() 0.
0.
所以,f(x)在(-![]() ,0)单调递减,在(0,+
,0)单调递减,在(0,+![]() )单调递增
)单调递增
(2)
【解答】由(I)知,对任意的m,f(x)在[-1,0]单调递减,在[0,1]单调递增,故f(x)在x=0处取得最小值。所以对于任意x1,x2![]() [-1,1],|f(x1)-f(x2)|
[-1,1],|f(x1)-f(x2)|![]() e-1的充要条件是:
e-1的充要条件是:![]() ,即
,即![]() ①,设函数g(t)=
①,设函数g(t)=![]() ,则g‘(t)=et-1,当t
,则g‘(t)=et-1,当t![]() 0时,g(t)
0时,g(t)![]() 0,当t
0,当t![]() 0时,g(t)
0时,g(t)![]() 0
0
故g(t)在(-![]() ,0)单调递减,在(0,+
,0)单调递减,在(0,+![]() )单调递增
)单调递增
又g(1)=0,g(-1)=![]() ,故当t
,故当t![]() [-1,1]时,g(t)
[-1,1]时,g(t)![]() 0,当m
0,当m![]() [-1,1]时,g(m)
[-1,1]时,g(m)![]() 0,g(-m)
0,g(-m)![]() 0,即①成立。
0,即①成立。
当m![]() 1时,由g(t)的单调性,g(m)
1时,由g(t)的单调性,g(m)![]() 0,即
0,即![]() ,当m
,当m![]() -1时,g(-m)
-1时,g(-m)![]() 0,即
0,即![]() ,
,
综上,m的取值范围是[-1,1].
【解析】(Ⅰ)先求导函数f‘(x)=m(emx-1)+2x,根据m的范围讨论导函数在(-![]() ,0)和(0,+
,0)和(0,+![]() )的符号即可;
)的符号即可;
(II)|f(x1)-f(x2)|![]() e-1恒成立,等价于|f(x1)-f(x2)|max
e-1恒成立,等价于|f(x1)-f(x2)|max![]() e-1。由x1:x2是两个独立的变量,故可求研究f(x)的值域,由(I)可得最小值为f(0)=1,最大值可能是f(-1)或f(1),故只需
e-1。由x1:x2是两个独立的变量,故可求研究f(x)的值域,由(I)可得最小值为f(0)=1,最大值可能是f(-1)或f(1),故只需![]() ,从而得关于m的不等式,因不易解出,故利用导数研究其单调性和符号,从而得解。
,从而得关于m的不等式,因不易解出,故利用导数研究其单调性和符号,从而得解。
【考点精析】认真审题,首先需要了解基本求导法则(若两个函数可导,则它们和、差、积、商必可导;若两个函数均不可导,则它们的和、差、积、商不一定不可导).


科目:高中数学 来源: 题型:
【题目】设正数x,y满足log ![]() x+log3y=m(m∈[﹣1,1]),若不等式3ax2﹣18xy+(2a+3)y2≥(x﹣y)2有解,则实数a的取值范围是( )
x+log3y=m(m∈[﹣1,1]),若不等式3ax2﹣18xy+(2a+3)y2≥(x﹣y)2有解,则实数a的取值范围是( )
A.(1, ![]() ]
]
B.(1, ![]() ]
]
C.[ ![]() ,+∞)
,+∞)
D.[ ![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C1的参数方程为 ![]() ,(其中φ为参数),曲线
,(其中φ为参数),曲线 ![]() ,以原点O为极点,x轴的正半轴为极轴建立极坐标系,射线l:θ=α(ρ≥0)与曲线C1 , C2分别交于点A,B(均异于原点O)
,以原点O为极点,x轴的正半轴为极轴建立极坐标系,射线l:θ=α(ρ≥0)与曲线C1 , C2分别交于点A,B(均异于原点O)
(1)求曲线C1 , C2的极坐标方程;
(2)当 ![]() 时,求|OA|2+|OB|2的取值范围.
时,求|OA|2+|OB|2的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 已知椭圆C:
已知椭圆C:![]() +
+![]() =1,(a
=1,(a![]() b
b![]() 0)的离心率为
0)的离心率为![]() ,点(2,
,点(2,![]() )在C上
)在C上
(1)求C的方程;
(2)直线l不经过原点O,且不平行于坐标轴,l与C有两个交点A,B,线段AB中点为M,证明:直线OM的斜率与直线l的斜率乘积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·新课标I卷)函数f(x)=cos(![]() x+
x+![]() )的部分图像如图所示,则f(x)的单调递减区间为( )
)的部分图像如图所示,则f(x)的单调递减区间为( )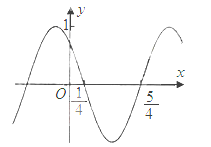
A.(k![]() -
-![]() ,k
,k![]() +
+![]() ), k
), k![]() Z
Z
B.(2k![]() -
-![]() ,2k
,2k![]() +
+![]() ),k
),k![]() Z
Z
C.(k-![]() ,k+
,k+![]() ), k
), k![]() Z
Z
D.(2k-![]() ,2k+
,2k+![]() ),k
),k![]() Z
Z
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·新课标I卷)选修4-1:几何证明选讲
如图AB是⊙O直径,AC是⊙O切线,BC交⊙O与点E.
(1)若D为AC中点,求证:DE是⊙O切线;
(2)若OA=![]() CE,求∠ACB的大小.
CE,求∠ACB的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·四川)已知A、B、C为△ABC的内角,tanA、tanB是关于方程x2+![]() px-p+1=0(p∈R)两个实根.
px-p+1=0(p∈R)两个实根.
(1)求C的大小
(2)若AB=1,AC=![]() ,求p的值
,求p的值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·湖南)已知抛物线C1:x2=4y的焦点F也是椭圆C2:![]() (a>b>0)的一个焦点,C1与C2的公共弦长为2
(a>b>0)的一个焦点,C1与C2的公共弦长为2![]() ,过点F的直线l与C1相交于A, B两点,与C2相交于C,D两点,且
,过点F的直线l与C1相交于A, B两点,与C2相交于C,D两点,且![]() 与
与![]() 同向.
同向.
(1)求C2的方程
(2)若|AC|=|BD|,求直线l的斜率
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com