
【题目】已知数列{an}的前n项和为Sn,2Sn+2n=an+1﹣2,a2=8,其中n∈N*.
(1)记bn=an+1,求证:{bn}是等比数列;
(2)设![]() 为数列{cn}的前n项和,若不等式k>Tn对任意的n∈N*恒成立,求实数k的取值范围.
为数列{cn}的前n项和,若不等式k>Tn对任意的n∈N*恒成立,求实数k的取值范围.
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:高中数学 来源: 题型:
【题目】已知直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() ,
,![]() ,线段
,线段![]() 的中垂线
的中垂线![]() 与抛物线
与抛物线![]() 有两个不同的交点
有两个不同的交点![]() 、
、![]() .
.
(1)求![]() 的取值范围;
的取值范围;
(2)是否存在![]() ,使得
,使得![]() ,
,![]() ,
,![]() ,
,![]() 四点共圆,若存在,请求出
四点共圆,若存在,请求出![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】交通拥堵指数是综合反映道路网畅通或拥堵的概念,记交通拥堵指数为![]() ,其范围为
,其范围为![]() ,分别有五个级别:
,分别有五个级别:![]() 畅通;
畅通;![]() 基本畅通;
基本畅通;![]() 轻度拥堵;
轻度拥堵;![]() 中度拥堵;
中度拥堵;![]() 严重拥堵.晚高峰时段(
严重拥堵.晚高峰时段(![]() ),从某市交通指挥中心选取了市区20个交通路段,依据其交通拥堵指数数据绘制的直方图如图所示.
),从某市交通指挥中心选取了市区20个交通路段,依据其交通拥堵指数数据绘制的直方图如图所示.
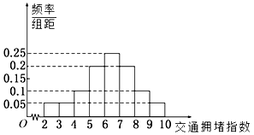
(Ⅰ)用分层抽样的方法从交通指数在![]() ,
,![]() ,
,![]() 的路段中共抽取
的路段中共抽取![]() 个路段,求依次抽取的三个级别路段的个数;
个路段,求依次抽取的三个级别路段的个数;
(Ⅱ)从(Ⅰ)中抽出的![]() 个路段中任取
个路段中任取![]() 个,求至少有
个,求至少有![]() 个路段为轻度拥堵的概率.
个路段为轻度拥堵的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)求f(x)的最小正周期和单调递减区间;
(Ⅱ)将函数f(x)的图象向右平移![]() 个单位,得到函数g(x)的图象,求g(x)在区间
个单位,得到函数g(x)的图象,求g(x)在区间![]() 上的值域.
上的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,曲线C1的参数方程为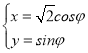 (
(![]() 为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为
为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为![]() ,曲线C2的极坐标方程为ρ=2sinθ.
,曲线C2的极坐标方程为ρ=2sinθ.
(1)探究直线l与曲线C2的位置关系,并说明理由;
(2)若曲线C3的极坐标方程为![]() ,且曲线C3与曲线C1、C2分别交于M、N两点,求|OM|2|ON|2的取值范围.
,且曲线C3与曲线C1、C2分别交于M、N两点,求|OM|2|ON|2的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 的右焦点到渐近线的距离为3.现有如下条件:①双曲线
的右焦点到渐近线的距离为3.现有如下条件:①双曲线![]() 的离心率为
的离心率为![]() ; ②双曲线
; ②双曲线![]() 与椭圆
与椭圆![]() 共焦点; ③双曲线右支上的一点
共焦点; ③双曲线右支上的一点![]() 到
到![]() 的距离之差是虚轴长的
的距离之差是虚轴长的![]() 倍.
倍.
请从上述3个条件中任选一个,得到双曲线![]() 的方程为_____________.
的方程为_____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=alnx-bx2,a,b∈R.若不等式f(x)≥x对所有的b∈(-∞,0],x∈(e,e2]都成立,则实数a的取值范围是( )
A. [e,+∞)B. [![]() ,+∞)
,+∞)
C. [![]() ,e2)D. [e2,+∞)
,e2)D. [e2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的上顶点为
的上顶点为![]() ,以
,以![]() 为圆心椭圆的长半轴为半径的圆与
为圆心椭圆的长半轴为半径的圆与![]() 轴的交点分别为
轴的交点分别为![]() ,
,![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设不经过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,试探究直线
,试探究直线![]() 是否过定点?若过定点,求出该定点的坐标,若不过定点,请说明理由.
是否过定点?若过定点,求出该定点的坐标,若不过定点,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com