
【题目】已知某校运动会男生组田径综合赛以选手三项运动的综合积分高低决定排名.具体积分规则如表1所示,某代表队四名男生的模拟成绩如表2.
表1 田径综合赛项目及积分规则
项目 | 积分规则 |
| 以 |
跳高 | 以 |
掷实心球 | 以 |
表2 某队模拟成绩明细
姓名 | 100米跑(秒) | 跳高(米) | 掷实心球(米) |
甲 |
|
|
|
乙 |
|
|
|
丙 |
|
|
|
丁 |
|
|
|
根据模拟成绩,该代表队应选派参赛的队员是:( )
A.甲B.乙C.丙D.丁
科目:高中数学 来源: 题型:
【题目】南宋数学家杨辉在《详解九章算法》和《算法通变本末》中,提出了一些新的垛积公式,所讨论的高阶等差数列与一般等差数列不同,前后两项之差并不相等,但是逐项差数之差或者高次差成等差数列对这类高阶等差数列的研究,在杨辉之后一般称为“垛积术”.现有高阶等差数列,其前7项分别为1,4,8,14,23,36,54,则该数列的第19项为( )(注:![]() )
)
A.1624B.1024C.1198D.1560
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,四边形
中,四边形![]() ,
,![]() 均为正方形,且
均为正方形,且![]() ,M为
,M为![]() 的中点,N为
的中点,N为![]() 的中点.
的中点.
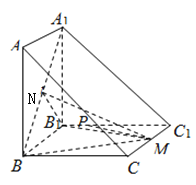
(1)求证:![]() 平面ABC;
平面ABC;
(2)求二面角![]() 的正弦值;
的正弦值;
(3)设P是棱![]() 上一点,若直线PM与平面
上一点,若直线PM与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求
,求![]() 的值
的值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 的焦点为
的焦点为![]() 和
和![]() ,过
,过![]() 的直线
的直线![]() 交
交![]() 于
于![]() 两点,过
两点,过![]() 作与
作与![]() 轴垂直的直线
轴垂直的直线![]() ,又知点
,又知点![]() ,直线
,直线![]() 记为
记为![]() ,
,![]() 与
与![]() 交于点
交于点![]() .设
.设![]() ,已知当
,已知当![]() 时,
时,![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)求证:无论![]() 如何变化,点
如何变化,点![]() 的横坐标是定值,并求出这个定值.
的横坐标是定值,并求出这个定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国全面二孩政策已于2016年1月1日起正式实施.国家统计局发布的数据显示,从2012年到2017年,中国的人口自然增长率变化始终不大,在5‰上下波动(如图).

为了了解年龄介于24岁至50岁之间的适孕夫妻对生育二孩的态度如何,统计部门按年龄分为9组,每组选取150对夫妻进行调查统计有生育二孩意愿的夫妻数,得到下表:
年龄区间 |
|
|
|
|
|
|
|
|
|
有意愿数 | 80 | 81 | 87 | 86 | 84 | 83 | 83 | 70 | 66 |
(1)设每个年龄区间的中间值为![]() ,有意愿数为
,有意愿数为![]() ,求样本数据的线性回归直线方程,并求该模型的相关系数
,求样本数据的线性回归直线方程,并求该模型的相关系数![]() (结果保留两位小数);
(结果保留两位小数);
(2)从![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 这五个年龄段中各选出一对夫妻(能代表该年龄段超过半数夫妻的意愿)进一步调研,再从这5对夫妻中任选2对夫妻.求其中恰有一对不愿意生育二孩的夫妻的概率.
这五个年龄段中各选出一对夫妻(能代表该年龄段超过半数夫妻的意愿)进一步调研,再从这5对夫妻中任选2对夫妻.求其中恰有一对不愿意生育二孩的夫妻的概率.
(参考数据和公式: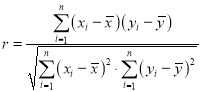 ,
,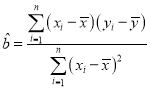 ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设有限数列![]() ,定义集合
,定义集合![]() 为数列
为数列![]() 的伴随集合.
的伴随集合.
(Ⅰ)已知有限数列![]() 和数列
和数列![]() .分别写出
.分别写出![]() 和
和![]() 的伴随集合;
的伴随集合;
(Ⅱ)已知有限等比数列![]() ,求
,求![]() 的伴随集合
的伴随集合![]() 中各元素之和
中各元素之和![]() ;
;
(Ⅲ)已知有限等差数列![]() ,判断
,判断![]() 是否能同时属于
是否能同时属于![]() 的伴随集合
的伴随集合![]() ,并说明理由.
,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中华人民共和国的国旗是五星红旗,旗面左上方缀着五颗黄色五角星,四颗小星环拱在一颗大星之后,并各有一个角尖正对大星的中心点,象征着中国共产党领导下的革命人民大团结和中国人民对党的衷心拥护.五角星可以通过正五边形连接对角线得到,如图所示,在正五边形ABCDE内部任取一点,则该点取自阴影部分的概率为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将字母![]() 放入
放入![]() 的方表格,每个格子各放一个字母,则每一行的字母互不相同,每一列的字母也互不相同的概率为_______;若共有
的方表格,每个格子各放一个字母,则每一行的字母互不相同,每一列的字母也互不相同的概率为_______;若共有![]() 行字母相同,则得k分,则所得分数
行字母相同,则得k分,则所得分数![]() 的数学期望为______;(注:横的为行,竖的为列;比如以下填法第二行的两个字母相同,第1,3行字母不同,该情况下
的数学期望为______;(注:横的为行,竖的为列;比如以下填法第二行的两个字母相同,第1,3行字母不同,该情况下![]() )
)
a | b |
c | c |
a | b |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列判断正确的是( )
A. “![]() ”是“
”是“![]() ”的充分不必要条件
”的充分不必要条件
B. 命题“若![]() ,则
,则![]() ”的否命题为“若
”的否命题为“若![]() ,则
,则![]() ”
”
C. 命题“![]() ,
,![]() ”的否定是“
”的否定是“![]() ,
,![]() ”
”
D. 若命题“![]() ”为假命题,则命题
”为假命题,则命题![]() ,
,![]() 都是假命题
都是假命题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com