
【题目】设椭圆![]() ,过点
,过点![]() 的直线
的直线![]() ,
,![]() 分别交
分别交![]() 于不同的两点
于不同的两点![]() 、
、![]() ,直线
,直线![]() 恒过点
恒过点![]()
(1)证明:直线![]() ,
,![]() 的斜率之和为定值;
的斜率之和为定值;
(2)直线![]() ,
,![]() 分别与
分别与![]() 轴相交于
轴相交于![]() ,
,![]() 两点,在
两点,在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() 为定值?若存在,求出点
为定值?若存在,求出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
 走进文言文系列答案
走进文言文系列答案科目:高中数学 来源: 题型:
【题目】某企业拥有3条相同的生产线,每条生产线每月至多出现一次故障.各条生产线是否出现故障相互独立,且出现故障的概率为![]() .
.
(1)求该企业每月有且只有1条生产线出现故障的概率;
(2)为提高生产效益,该企业决定招聘名维修工人及时对出现故障的生产线进行维修.已知每名维修工人每月只有及时维修1条生产线的能力,且每月固定工资为1万元.此外,统计表明,每月在不出故障的情况下,每条生产线创造12万元的利润;如果出现故障能及时维修,每条生产线创造8万元的利润;如果出现故障不能及时维修,该生产线将不创造利润,以该企业每月实际获利的期望值为决策依据,在![]() 与
与![]() 之中选其一,应选用哪个?(实际获利=生产线创造利润-维修工人工资)
之中选其一,应选用哪个?(实际获利=生产线创造利润-维修工人工资)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某省在2017年启动了“3+3”高考模式.所谓“3+3”高考模式,就是语文、数学、外语(简称语、数、外)为高考必考科目,从物理、化学、生物、政治、历史、地理(简称理、化、生、政、史、地)六门学科中任选三门作为选考科目.该省某中学2017级高一新生共有990人,学籍号的末四位数从0001到0990.
(1)现从高一学生中抽样调查110名学生的选考情况,问:采用什么样的抽样方法较为恰当?(只写出结论,不需要说明理由)
(2)据某教育机构统计,学生所选三门学科在将来报考专业时受限制的百分比是不同的.该机构统计了受限百分比较小的十二种选择的百分比值![]() ,制作出如下条形图.
,制作出如下条形图.

设以上条形图中受限百分比的均值为![]() ,标准差为
,标准差为![]() .如果一个学生所选三门学科专业受限百分比在区间
.如果一个学生所选三门学科专业受限百分比在区间![]() 内,我们称该选择为“恰当选择”.该校李明同学选择了化学,然后从余下五门选考科目中任选两门.问李明的选择为“恰当选择"的概率是多少?(均值
内,我们称该选择为“恰当选择”.该校李明同学选择了化学,然后从余下五门选考科目中任选两门.问李明的选择为“恰当选择"的概率是多少?(均值![]() ,标准差
,标准差![]() 均精确到0.1)
均精确到0.1)
(参考公式和数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“干支纪年法”是中国历法上自古以来就一直使用的纪年方法,甲、乙、丙、丁、戊、己、庚、辛、壬、癸被称为“十天干”,子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥叫做“十二地支”.“天干”以“甲”字开始,“地支”以“子”字开始,两者按照干支顺序相配,构成了“干支纪年法”,其相配顺序为:甲子、乙丑、丙寅![]() 癸酉、甲戌、乙亥、丙子
癸酉、甲戌、乙亥、丙子![]() 癸未、甲申、乙酉、丙戌
癸未、甲申、乙酉、丙戌![]() 癸巳
癸巳![]() 癸亥,60为一个周期,周而复始,循环记录.按照“干支纪年法”,中华人民共和国成立的那年为己丑年,则2013年为( )
癸亥,60为一个周期,周而复始,循环记录.按照“干支纪年法”,中华人民共和国成立的那年为己丑年,则2013年为( )
A.甲巳年B.壬辰年C.癸巳年D.辛卯年
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,
中,![]() ,
,![]() 是曲线段
是曲线段![]() :
:![]() (
(![]() 是参数,
是参数,![]() )的左、右端点,
)的左、右端点,![]() 是
是![]() 上异于
上异于![]() ,
,![]() 的动点,过点
的动点,过点![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() .
.
(1)建立适当的极坐标系,写出点![]() 轨迹的极坐标方程;
轨迹的极坐标方程;
(2)求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数g(x)=![]() ,f(x)=g'(x)-
,f(x)=g'(x)-![]() (a是常数).若对a∈R,函数h(x)=kx(k是常数)的图象与曲线y=f(x)总相切于一个定点.
(a是常数).若对a∈R,函数h(x)=kx(k是常数)的图象与曲线y=f(x)总相切于一个定点.
(1)求k的值;
(2)若对![]() ∈(0,+∞),[f(
∈(0,+∞),[f(![]() )-h(
)-h(![]() )][f(
)][f(![]() )-h(
)-h(![]() )]>0,求实数a的取值范围.
)]>0,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年是新中国成立七十周年,新中国成立以来,我国文化事业得到了充分发展,尤其是党的十八大以来,文化事业发展更加迅速,下图是从2013 年到 2018 年六年间我国公共图书馆业机构数(个)与对应年份编号的散点图(为便于计算,将 2013 年编号为 1,2014 年编号为 2,…,2018年编号为 6,把每年的公共图书馆业机构个数作为因变量,把年份编号从 1 到 6 作为自变量进行回归分析),得到回归直线![]() ,其相关指数
,其相关指数![]() ,给出下列结论,其中正确的个数是( )
,给出下列结论,其中正确的个数是( )
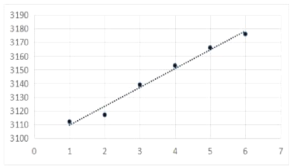
①公共图书馆业机构数与年份的正相关性较强
②公共图书馆业机构数平均每年增加13.743个
③可预测 2019 年公共图书馆业机构数约为3192个
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x),若存在x0,使得f(x0)=x0,则称x0是函数y=f(x)的一个不动点,设二次函数f(x)=ax2+(b+1)x+b-2
(Ⅰ)当a=2,b=1时,求函数f(x)的不动点;
(Ⅱ)若对于任意实数b,函数f(x)恒有两个不同的不动点,求实数a的取值范围;
(Ⅲ)在(Ⅱ)的条件下,若函数y=f(x)的图象上A,B两点的横坐标是函数f(x)的不动点,且直线![]() 是线段AB的垂直平分线,求实数b的取值范围.
是线段AB的垂直平分线,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在平面直角坐标系![]() 中,中心在原点,焦点在y轴上的椭圆C与椭圆
中,中心在原点,焦点在y轴上的椭圆C与椭圆![]() 的离心率相同,且椭圆C短轴的顶点与椭圆E长轴的顶点重合.
的离心率相同,且椭圆C短轴的顶点与椭圆E长轴的顶点重合.
(1)求椭圆C的方程;
(2)若直线l与椭圆E有且仅有一个公共点,且与椭圆C交于不同两点A,B,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com