
【题目】如图,在四棱锥P﹣ABCD中,底面四边形ABCD内接于圆O,AC是圆O的一条直径,PA⊥平面ABCD,PA=AC=2,E是PC的中点,∠DAC=∠AOB 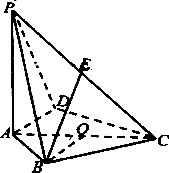
(1)求证:BE∥平面PAD;
(2)若二面角P﹣CD﹣A的正切值为2,求直线PB与平面PCD所成角的正弦值.
【答案】
(1)证明:∵,∠DAC=∠AOB
∴AD∥OB,
∵E是PC的中点,O是AC的中点,
∴OE是△PAC的中位线,
∴OE∥PA,
∵PA∩AD=A,
平面OBE∥平面PAD,
∵BE平面PAD,BE平面PAD,
∴BE∥平面PAD
(2)解:∵AC是圆O的一条直径,∴AC⊥AD,
∵PA⊥平面ABCD,∴PA⊥CD,
则CD⊥平面PAD,
则CD⊥PD,
则∠PDA是二面角P﹣CD﹣A的平面角,
若二面角P﹣CD﹣A的正切值为2,
则tan∠PDA= ![]() =2,
=2,
即AD=1,
建立以D为坐标原点,DA,DC,垂直于平面ABCD的直线分别为x,y,z轴的空间直角坐标系如图:
则B( ![]() ,
, ![]() ,0),P(1,0,2),
,0),P(1,0,2), ![]() =(-
=(- ![]() ,﹣
,﹣ ![]() ,2)
,2)
D(0,0,0),C(0, ![]() ,0),
,0),
则 ![]() =(0,
=(0, ![]() ,0),
,0), ![]() =(1,0,2),
=(1,0,2),
设平面PCD的法向量为 ![]() =(x,y,z),
=(x,y,z),
则 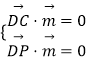 ,即
,即 ![]() ,令z=1,则x=﹣2,y=0,
,令z=1,则x=﹣2,y=0,
即 ![]() =(﹣2,0,1),
=(﹣2,0,1),
则直线PB与平面PCD所成角的正弦值sin< ![]() ,
, ![]() >=|cos<
>=|cos< ![]() ,
, ![]() >|=|
>|=| 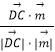 |=
|= ![]()
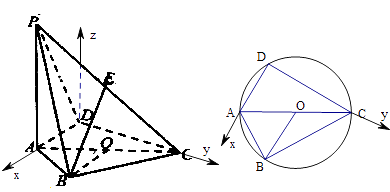
【解析】(1)根据面面平行的性质定理证明平面OBE∥平面PAD,即可证明BE∥平面PAD;(2)建立空间坐标系,根据二面角P﹣CD﹣A的正切值为2,得到AD=1,然后求出平面的法向量,利用直线和平面所成角的定义即可求直线PB与平面PCD所成角的正弦值
【考点精析】本题主要考查了直线与平面平行的判定的相关知识点,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行才能正确解答此题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥S﹣ABCD,SB⊥AD,侧面SAD是边长为4的等边三角形,底面ABCD为菱形,侧面SAD与底面ABCD所成的二面角为120°.
(1)求点S到平面ABCD的距离;
(2)若E为SC的中点,求二面角A﹣DE﹣C的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C:ρsin2θ=2acosθ(a>0),直线l的参数方程为  (t为参数),l与C分别交于M,N,P(﹣2,﹣4).
(t为参数),l与C分别交于M,N,P(﹣2,﹣4).
(1)写出C的平面直角坐标系方程和l的普通方程;
(2)已知|PM|,|MN|,|PN|成等比数列,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() 图象上有且仅有四个不同的点关于直线y=e的对称点在函数g(x)=kx+2e+1的图象上,则实数k的取值范围为( )
图象上有且仅有四个不同的点关于直线y=e的对称点在函数g(x)=kx+2e+1的图象上,则实数k的取值范围为( )
A.(1,2)
B.(﹣1,0)
C.(﹣2,﹣1)
D.(﹣6,﹣1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两俱乐部举行乒乓球团体对抗赛.双方约定:
①比赛采取五场三胜制(先赢三场的队伍获得胜利.比赛结束)
②双方各派出三名队员.前三场每位队员各比赛﹣场
已知甲俱乐部派出队员A1、A2 . A3 , 其中A3只参加第三场比赛.另外两名队员A1、A2比赛场次未定:乙俱乐部派出队员B1、B2 . B3 , 其中B1参加第一场与第五场比赛.B2参加第二场与第四场比赛.B3只参加第三场比赛
根据以往的比赛情况.甲俱乐部三名队员对阵乙俱乐部三名队员获胜的概率如表:
A1 | A2 | A3 | |
B1 |
|
|
|
B2 |
|
|
|
B3 |
|
|
|
(1)若甲俱乐部计划以3:0取胜.则应如何安排A1、A2两名队员的出场顺序.使得取胜的概率最大?
(2)若A1参加第一场与第四场比赛,A2参加第二场与第五场比赛,各队员每场比赛的结果互不影响,设本次团体对抗赛比赛的场数为随机变量X,求X的分布列及数学期望E(X)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax﹣ ![]() x2﹣aln(x+1)(a>0),g(x)=ex﹣x﹣1,曲线y=f(x)与y=g(x)在原点处的公共的切线.
x2﹣aln(x+1)(a>0),g(x)=ex﹣x﹣1,曲线y=f(x)与y=g(x)在原点处的公共的切线.
(1)若x=0为函数f(x)的极大值点,求f(x)的单调区间(用a表示);
(2)若x≥0,g(x)≥f(x)+ ![]() x2 , 求a的取值范围.
x2 , 求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,我国许多省市雾霾天气频发,为增强市民的环境保护意识,某市面向全市征召n名义务宣传志愿者,成立环境保护宣传组织![]() 现把该组织的成员按年龄分成5组:第1组
现把该组织的成员按年龄分成5组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示,已知第2组有70人.
,得到的频率分布直方图如图所示,已知第2组有70人.
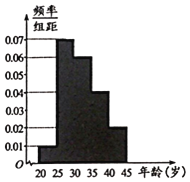
(1)求该组织的人数.
(2)若从第3,4,5组中用分层抽样的方法抽取6名志愿者参加某社区的宣传活动,然后在这6名志愿者中随机抽取2名志愿者介绍宣传经验,求第3组至少有一名志愿者被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某重点中学将全部高一学生分成![]() 两个成绩相当(成绩的均值、方差都相同)的级部,
两个成绩相当(成绩的均值、方差都相同)的级部, ![]() 级部采用传统形式的教学方式,
级部采用传统形式的教学方式, ![]() 级部采用新型的基于信息化的自主学习教学方式.为了解教学效果,期末考试后分别从两个级部中各随机抽取30名学生的数学成绩进行统计,做出茎叶图如下,记成绩不低于127分者为“优秀”.
级部采用新型的基于信息化的自主学习教学方式.为了解教学效果,期末考试后分别从两个级部中各随机抽取30名学生的数学成绩进行统计,做出茎叶图如下,记成绩不低于127分者为“优秀”.
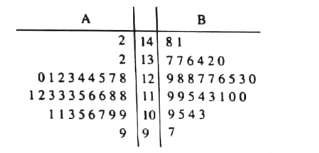
(1)在![]() 级部样本的30个个体中随机抽取1个,求抽出的为“优秀”的概率;
级部样本的30个个体中随机抽取1个,求抽出的为“优秀”的概率;
(2)由以上数据填写下面列联表,并判断是否有![]() 的把握认为“优秀”与教学方式有关.
的把握认为“优秀”与教学方式有关.
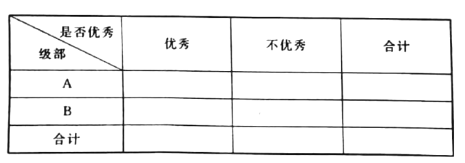
附表:

附: 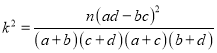 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com