
【题目】一个口袋内装有大小相同的7个白球和1个黑球.
(1)从口袋内取出3个球,共有多少种取法?
(2)从口袋内取出3个球,使其中含有1个黑球,有多少种取法?
(3)从口袋内取出3个球,使其中不含黑球,有多少种取法?
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代数学成就的杰出代表作之一,其中《方田》章给出计算弧田面积所用的经验公式为:弧田面积![]() (弦
(弦![]() 矢
矢![]() 矢
矢![]() ),弧田(如图)由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,现有圆心角为
),弧田(如图)由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,现有圆心角为![]() ,半径等于6米的弧田,按照上述经验公式计算所得弧田面积约为( )
,半径等于6米的弧田,按照上述经验公式计算所得弧田面积约为( )
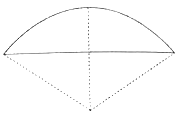
A.12平方米B.16平方米C.20平方米D.24平方米
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设![]() ,
,![]() 分别是正方体
分别是正方体![]() 的棱
的棱![]() 上两点,且
上两点,且![]() ,
,![]() ,其中正确的命题为( )
,其中正确的命题为( )
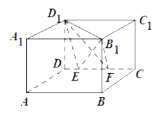
A.三棱锥![]() 的体积为定值
的体积为定值
B.异面直线![]() 与
与![]() 所成的角为
所成的角为![]()
C.![]() 平面
平面![]()
D.直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在2018年俄罗斯世界杯期间,莫斯科的部分餐厅经营了来自中国的小龙虾,这些小龙虾标有等级代码.为得到小龙虾等级代码数值![]() 与销售单价
与销售单价![]() 之间的关系,经统计得到如下数据:
之间的关系,经统计得到如下数据:
等级代码数值 | 38 | 48 | 58 | 68 | 78 | 88 |
销售单价 | 16.8 | 18.8 | 20.8 | 22.8 | 24 | 25.8 |
(1)已知销售单价![]() 与等级代码数值
与等级代码数值![]() 之间存在线性相关关系,求
之间存在线性相关关系,求![]() 关于
关于![]() 的线性回归方程(系数精确到0.1);
的线性回归方程(系数精确到0.1);
(2)若莫斯科某个餐厅打算从上表的6种等级的中国小龙虾中随机选2种进行促销,记被选中的2种等级代码数值在60以下(不含60)的数量为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
参考公式:对一组数据![]() ,
,![]() ,
,![]() ,其回归直线
,其回归直线![]() 的斜率和截距最小二乘估计分别为:
的斜率和截距最小二乘估计分别为: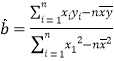 ,
,![]() .
.
参考数据:![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在单位正![]() 内任取一点P,以PA、PB、PC为边生成
内任取一点P,以PA、PB、PC为边生成![]() .
.
(1)当![]() 分别为锐角三角形、直角三角形、钝角三角形时,求出点P的轨迹.
分别为锐角三角形、直角三角形、钝角三角形时,求出点P的轨迹.
(2)证明:当![]() 的周长取最小值时,面积取最大值.
的周长取最小值时,面积取最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com