
| A. | y=cos2x-sin2x | B. | y=sin2x+cos2x | C. | y=cos2x-sin2x | D. | y=sin2x+cosx |
分析 利用三角恒等变换化简函数的解析式,再利用三角函数的奇偶性和周期性逐一判断各个选项是否正确,从而得出结论.
解答 解:y=cos2x-sin2x=cos2x-$\frac{1-cos2x}{2}$=$\frac{3}{2}$cos2x-$\frac{1}{2}$ 是偶函数,它的周期为$\frac{2π}{2}$=π,满足条件;
而y=sin2x+cos2x=$\sqrt{2}$sin(2x+$\frac{π}{4}$) 和 y=cos2x-sin2x=$\sqrt{2}$cos(2x+$\frac{π}{4}$)都是非奇非偶函数,
故排除B、C,
y=sin2x+cosx=-cos2x+cosx+1=-${(cosx-\frac{1}{2})}^{2}$+$\frac{5}{4}$不是偶函数,故排除D,
故选:A.
点评 本题主要考查三角恒等变换,三角函数的奇偶性和周期性,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
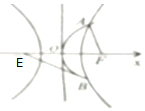 已知E,F为双曲线$C:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(0<a<b)$的左右焦点,抛物线y2=2px(p>0)与双曲线有公共的焦点F,且与双曲线交于A、B不同两点,若5|AF|=4|EF|,则双曲线的离心率为( )
已知E,F为双曲线$C:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(0<a<b)$的左右焦点,抛物线y2=2px(p>0)与双曲线有公共的焦点F,且与双曲线交于A、B不同两点,若5|AF|=4|EF|,则双曲线的离心率为( )| A. | $4+\sqrt{7}$ | B. | $4-\sqrt{3}$ | C. | $4+\sqrt{3}$ | D. | $4-\sqrt{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
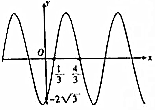
| A. | 函数f(x)的最小正周期为π | |
| B. | 函数f(x)的值域为[-$\frac{7}{2}$,$\frac{7}{2}$] | |
| C. | 函数f(x)的图象关于直线x=-$\frac{1}{6}$对称 | |
| D. | 函数f(x)的图象向右平移$\frac{1}{3}$个单位得到函数y=Asinωx的图象 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
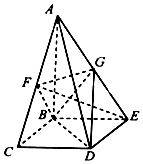 如图所示,在四棱锥A-BCDE中,AB⊥平面BCDE,四边形BCDE为矩形,F、G分别为AC、AE的中点,AB=BC=2,BE=$\sqrt{2}$.
如图所示,在四棱锥A-BCDE中,AB⊥平面BCDE,四边形BCDE为矩形,F、G分别为AC、AE的中点,AB=BC=2,BE=$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com