
| A. | (x-3)2+(y-1)2=9 | B. | (x+3)2+(y+1)2=9 | C. | ${({x-4})^2}+{({y-\frac{4}{3}})^2}=16$ | D. | (x-6)2+(y-2)2=9 |
分析 由圆心在直线$y=\frac{1}{3}x$上,设出圆心坐标,再根据圆与y轴相切,得到圆心到y轴的距离即圆心横坐标的绝对值等于圆的半径,表示出半径r,由弦长的一半,圆的半径r及表示出的d利用勾股定理列出关于t的方程,求出方程的解得到t的值,从而得到圆心坐标和半径,根据圆心和半径写出圆的方程即可.
解答 解:设圆心为(3t,t),半径为r=|3t|,
∵圆C截x轴所得弦的长为$4\sqrt{2}$,
∴t2+8=9t2,
∴t=±1,
∵圆C与y轴的正半轴相切,
∴t=-1不符合题意,舍去,
故t=1,3t=3,
∴(x-3)2+(y-1)2=9.
故选A.
点评 此题综合考查了垂径定理,勾股定理及点到直线的距离公式.根据题意设出圆心坐标,找出圆的半径是解本题的关键.


科目:高中数学 来源: 题型:选择题
| A. | 0≤α≤$\frac{π}{4}$ | B. | $\frac{π}{2}$<α<π | C. | $\frac{π}{4}$≤α<$\frac{π}{2}$ | D. | $\frac{π}{2}$<α≤$\frac{3π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
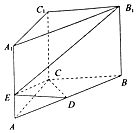 如图所示,在直三棱柱ABC-A1B1C1中,底面ABC是等腰直角三角形,且斜边AB=2$\sqrt{2}$,侧棱AA1=4,点D为AB的中点,点E在线段AA1上,AE=λAA1(λ∈R).
如图所示,在直三棱柱ABC-A1B1C1中,底面ABC是等腰直角三角形,且斜边AB=2$\sqrt{2}$,侧棱AA1=4,点D为AB的中点,点E在线段AA1上,AE=λAA1(λ∈R).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
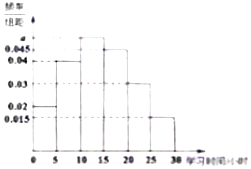 某市教育局随机调查了300名高中学生周末的学习时间(单位:小时),制成了如图所示的频率分布直方图,其中学习时间的范围是[0,30],样本数据分组为,[0,5),[5,10),[10,15),[15,20),[20,25),[25,30],根据直方图,这300名高中生周末的学习时间是[5,15)小时的人数是( )
某市教育局随机调查了300名高中学生周末的学习时间(单位:小时),制成了如图所示的频率分布直方图,其中学习时间的范围是[0,30],样本数据分组为,[0,5),[5,10),[10,15),[15,20),[20,25),[25,30],根据直方图,这300名高中生周末的学习时间是[5,15)小时的人数是( )| A. | 15 | B. | 27 | C. | 135 | D. | 165 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com