
【题目】如图,棱形![]() 与正三角形
与正三角形![]() 的边长均为2,它们所在平面互相垂直,
的边长均为2,它们所在平面互相垂直, ![]() ,且
,且![]() .
.
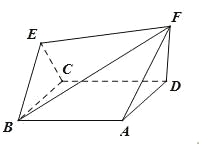
(1)求证: ![]() ;
;
(2)若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知等差数列{an}中公差d≠0,有a1+a4=14,且a1,a2,a7成等比数列.
(Ⅰ)求{an}的通项公式an与前n项和公式Sn;
(Ⅱ)令bn=![]() (k<0),若{bn}是等差数列,求数列{
(k<0),若{bn}是等差数列,求数列{![]() }的前n项和Tn.
}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用长为![]() ,宽为
,宽为![]() 的长方形铁皮做一个无盖的容器.先在四角分别截去一个小正方形,然后把四边翻转
的长方形铁皮做一个无盖的容器.先在四角分别截去一个小正方形,然后把四边翻转![]() ,再焊接而成(如图).问该容器的高为多少时,容器的容积最大?最大容积是多少?
,再焊接而成(如图).问该容器的高为多少时,容器的容积最大?最大容积是多少?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前3项和为6,前8项和为-4.
(1)求数列{an}的通项公式;
(2)设bn=(4-an)qn-1 (q≠0,n∈N*),求数列{bn}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=elnx,g(x)=![]() f(x)-(x+1).(e=2.718……)
f(x)-(x+1).(e=2.718……)
(1)求函数g(x)的极大值;
(2)求证:1+![]() +
+![]() +…+
+…+![]() >ln(n+1)(n∈N*).
>ln(n+1)(n∈N*).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的方程为
的方程为![]() ,两焦点
,两焦点![]() ,点
,点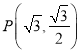 在椭圆
在椭圆![]() 上.
上.
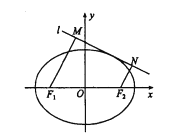
(1)求椭圆![]() 的方程;
的方程;
(2)如图,动直线![]() 与椭圆
与椭圆![]() 有且仅有一个公共点,点
有且仅有一个公共点,点![]() 、
、![]() 是直线
是直线![]() 上的两点,且
上的两点,且![]() .求四边形
.求四边形![]() 面积
面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是单调减函数,若将方程
是单调减函数,若将方程![]() 与
与![]() 的解分别称为函数
的解分别称为函数![]() 的不动点与稳定点.则“
的不动点与稳定点.则“![]() 是
是![]() 的不动点”是“
的不动点”是“![]() 是
是![]() 的稳定点”的 ( )
的稳定点”的 ( )
A.充要条件 B.充分不必要条件
C.必要不充分条件 D.既不充分也不必要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com