
分析 (1)设圆心坐标为(a,b),则$\left\{\begin{array}{l}{(a-1)^2}+{(b-3)^2}={r^2}\\{(a-3)^2}+{(b-2)^2}={r^2}\\ a+b-3=0\end{array}\right.$,即可求圆C的方程;
(2)令z=x+y,即y=-x+z,当这条直线与圆相切时,它在y轴上的截距最大或最小.
解答 解:(1)设圆心坐标为(a,b),则$\left\{\begin{array}{l}{(a-1)^2}+{(b-3)^2}={r^2}\\{(a-3)^2}+{(b-2)^2}={r^2}\\ a+b-3=0\end{array}\right.$
解得:a=1,b=2,r=2,故圆的方程为:(x-1)2+(y-2)2=4…(6分)
(2)令z=x+y,即y=-x+z,当这条直线与圆相切时,它在y轴上的截距最大或最小,
圆心到直线的距离d=$\frac{|1+2-z|}{\sqrt{2}}$=2,z=3±2$\sqrt{2}$,∴最大值为:$3+2\sqrt{2}$…(12分)
点评 本题考查圆的方程,考查直线与圆的位置关系,求出圆的方程是关键.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:高中数学 来源: 题型:选择题
| A. | a≤2 | B. | a≤1 | C. | a≤-1 | D. | a≤0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=2x-1.5 | B. | y=0.8x+3.3 | C. | y=-2x+14.5 | D. | y=-0.6x+9.1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
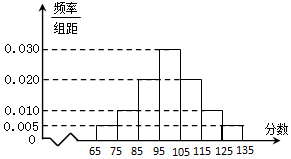 某校高二年级在一次数学测验后,随机抽取了部分学生的数学成绩组成一个样本,得到如下频率分布直方图:
某校高二年级在一次数学测验后,随机抽取了部分学生的数学成绩组成一个样本,得到如下频率分布直方图:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某园林公司准备绿化一块半径为200米,圆心角为$\frac{π}{4}$的扇形空地(如图的扇形OPQ区域),扇形的内接矩形ABCD为一水池,其余的地方种花,若∠COP=α,矩形ABCD的面积为S(单位:平方米).
某园林公司准备绿化一块半径为200米,圆心角为$\frac{π}{4}$的扇形空地(如图的扇形OPQ区域),扇形的内接矩形ABCD为一水池,其余的地方种花,若∠COP=α,矩形ABCD的面积为S(单位:平方米).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com