
【题目】已知函数fn(x)= ![]() x3﹣
x3﹣ ![]() (n+1)x2+x(n∈N*),数列{an}满足an+1=f'n(an),a1=3.
(n+1)x2+x(n∈N*),数列{an}满足an+1=f'n(an),a1=3.
(1)求a2 , a3 , a4;
(2)根据(1)猜想数列{an}的通项公式,并用数学归纳法证明;
(3)求证: ![]() +
+ ![]() +…+
+…+ ![]() <
< ![]() .
.
【答案】
(1)解: ![]() ,a1=3,又
,a1=3,又 ![]() ,
,
∴ ![]() ,
, ![]() ,
, ![]()
(2)解:猜想an=n+2,用数学归纳法证明:
当n=1时显然成立,
假设当n=k(k∈N*)时,ak=k+2,
则当n=k+1(k∈N*)时,
ak+1=ak2﹣(k+1)ak+1=(k+2)2﹣(k+1)(k+2)+1,
=k+3=(k+1)+2,
∴当n=k(k∈N*)时,猜想成立.
根据数学归纳法对一切n∈N*,an=n+2均成立
(3)证明:当k≥2时,有 ![]() <
< ![]() ,
,
∴n≥2时,有 ![]() <1+
<1+ ![]() [(1﹣
[(1﹣ ![]() )+(
)+( ![]() ﹣
﹣ ![]() )+…(
)+…( ![]() ﹣
﹣ ![]() )]
)]
=1+ ![]() (1﹣
(1﹣ ![]() )<1+
)<1+ ![]() =
= ![]() .
.
又n=1时, ![]() =1<
=1< ![]() .
.
故对一切n∈N*,有 ![]() <
< ![]()
【解析】(1)先求导,再根据递推公式分别求出a2 , a3 , a4;(2)利用数学归纳法证明即可,(3)利用裂项求和和放缩法即可证明.
【考点精析】解答此题的关键在于理解数学归纳法的定义的相关知识,掌握数学归纳法是证明关于正整数n的命题的一种方法.


科目:高中数学 来源: 题型:
【题目】中国古代儒家要求学生掌握六种基本才艺:礼、乐、射、御、书、数,简称“六艺”,某中学为弘扬“六艺”的传统文化,分别进行了主题为“礼、乐、射、御、书、数”六场传统文化知识的竞赛,现有甲、乙、丙三位选手进入了前三名的最后角逐、规定:每场知识竞赛前三名的得分都分别为![]() (
(![]() ,且
,且![]() );选手最后得分为各场得分之和,在六场比赛后,已知甲最后得分为26分,乙和丙最后得分都为11分,且乙在其中一场比赛中获得第一名,则下列推理正确的是( )
);选手最后得分为各场得分之和,在六场比赛后,已知甲最后得分为26分,乙和丙最后得分都为11分,且乙在其中一场比赛中获得第一名,则下列推理正确的是( )
A. 每场比赛第一名得分![]() 为4 B. 甲可能有一场比赛获得第二名
为4 B. 甲可能有一场比赛获得第二名
C. 乙有四场比赛获得第三名 D. 丙可能有一场比赛获得第一名
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱ABC﹣A1B1C1 , 底面△ABC中,CA=CB=1,∠BCA=90°,棱AA1=2,M、N分别为A1B1、A1A的中点. 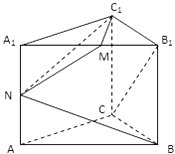
(1)求 ![]() >的值;
>的值;
(2)求证:BN⊥平面C1MN;
(3)求点B1到平面C1MN的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() x2﹣3x+(a﹣1)lnx,g(x)=ax,h(x)=f(x)﹣g(x)+3x.
x2﹣3x+(a﹣1)lnx,g(x)=ax,h(x)=f(x)﹣g(x)+3x.
(1)当a=5时,求函数f(x)的导函数f′(x)的最小值;
(2)当a=3时,求函数h(x)的单调区间及极值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《莱因德纸草书》(Rhind Papyrus)是世界上最古老的数学著作之一.书中有一道这样的题目:把100个面包分给5个人,使每个人所得成等差数列,且使较大的三份之和的 ![]() 是较小的两份之和,问最小一份为( )
是较小的两份之和,问最小一份为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】二维空间中圆的一维测度(周长)l=2πr,二维测度(面积)S=πr2;三维空间中球的二维测度(表面积)S=4πr2 , 三维测度(体积)V= ![]() πr3;四维空间中“超球”的三维测度V=8πr3 , 则猜想其四维测度W= .
πr3;四维空间中“超球”的三维测度V=8πr3 , 则猜想其四维测度W= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() ,定义椭圆的“伴随圆”方程为
,定义椭圆的“伴随圆”方程为![]() ;若抛物线
;若抛物线![]() 的焦点与椭圆C的一个短轴端点重合,且椭圆C的离心率为
的焦点与椭圆C的一个短轴端点重合,且椭圆C的离心率为![]() .
.
(1)求椭圆C的方程和“伴随圆”E的方程;
(2)过“伴随圆”E上任意一点P作椭圆C的两条切线PA,PB,A,B为切点,延长PA与“伴随圆”E交于点Q,O为坐标原点.
(i)证明:PA⊥PB;
(ii)若直线OP,OQ的斜率存在,设其分别为![]() ,试判断
,试判断![]() 是否为定值,若是, 求出该值;若不是,请说明理由.
是否为定值,若是, 求出该值;若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com