
分析 (1)设等差数列{an}的公差为d,运用等差数列的通项公式和性质,求得首项和公差,即可得到所求通项公式;
(2)运用等比数列中项性质可得a3=2,a1=-4,a2=-1,进而得到an+7=3n,运用等差数列的求和公式即可得到所求和.
解答 解:(1)设等差数列{an}的公差为d,
由a1+a2+a3=-3,a1•a2•a3=8.
可得3a1+3d=-3,即a2=-1,
a1+a3=-2,a1•a3=-8.
解得a1=-4,a3=2或a1=2,a3=-4,
则d=3或-3,
则an=-4+3(n-1)=3n-7;或an=2-3(n-1)=5-3n;
(2)a2,a3,a1成等比数列,
可得a32=a1a2,
又a1•a2•a3=8,可得a3=2,a1=-4,a2=-1,
则an+7=3n,
可得{an+7}的前n项和为$\frac{1}{2}$n(3+3n)=$\frac{3}{2}$(n2+n).
点评 本题考查等差数列的通项公式和求和公式的运用,考查等比数列中项的性质,考查方程思想和化简整理的运算能力,属于基础题.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:选择题
| A. | f′(2)<0 | B. | f′(2)=0 | C. | f′(2)>0 | D. | f′(2)不存在 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\;0\;,\;\frac{2}{3}\;)$ | B. | $(\;0\;,\;\frac{1}{2}\;]$ | C. | $[\;\frac{1}{3}\;,\;1\;)$ | D. | $[\;\frac{1}{2}\;,\;1\;)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 1 | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m∥n,n?α,则 m∥α | B. | 若α⊥β,α∩β=m,m⊥n,则 n⊥α | ||
| C. | 若l⊥n,m⊥n,则 l∥m | D. | 若l⊥α,m⊥β,且 l⊥m,则 α⊥β |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $1+\sqrt{π}$ | B. | 1+$\frac{1}{{\sqrt{π}}}$ | C. | $1+\frac{1}{{\sqrt{2π}}}$ | D. | $1+\frac{1}{{2\sqrt{π}}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
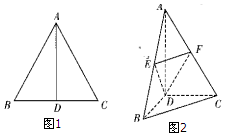 如图,边长为2的等边三角形ABC中,D为BC的中点,将△ABC沿AD翻折成直二面角B-AD-C,点E,F分别是AB,AC的中点.
如图,边长为2的等边三角形ABC中,D为BC的中点,将△ABC沿AD翻折成直二面角B-AD-C,点E,F分别是AB,AC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com