
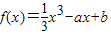 ,其中实数a,b是常数.
,其中实数a,b是常数.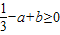 ,即
,即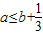 :①当a=0时,b=0,1,2都满足;②当a=1时,b=1,2满足;③当a=2时,b=2满足.
:①当a=0时,b=0,1,2都满足;②当a=1时,b=1,2满足;③当a=2时,b=2满足. =
= .
.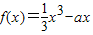 ,f′(x)=x2-a.
,f′(x)=x2-a.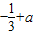 ;
;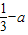 .
. ,∴f′(x)=x2-1,当x∈(0,1]时,f′(x)<0;当x∈(1,2]时,f′(x)>0.
,∴f′(x)=x2-1,当x∈(0,1]时,f′(x)<0;当x∈(1,2]时,f′(x)>0.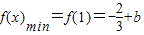 .
.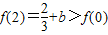 ,当x∈[0,2]时,
,当x∈[0,2]时,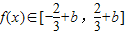 .
.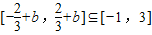 .
.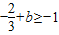 且
且 ,解得
,解得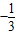
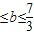


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源:2013-2014学年山东省日照市高三12月校际联考文科数学试卷(解析版) 题型:解答题
已知函数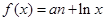 ,其中实数a为常数.
,其中实数a为常数.
(I)当a=-l时,确定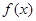 的单调区间:
的单调区间:
(II)若f(x)在区间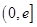 (e为自然对数的底数)上的最大值为-3,求a的值;
(e为自然对数的底数)上的最大值为-3,求a的值;
(Ⅲ)当a=-1时,证明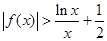 .
.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东省中山市高三(上)期末数学试卷(文科)(解析版) 题型:解答题
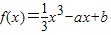 ,其中实数a,b是常数.
,其中实数a,b是常数.查看答案和解析>>
科目:高中数学 来源:2013年广东省中山市重点中学高考数学一模试卷(文科)(解析版) 题型:解答题
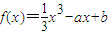 ,其中实数a,b是常数.
,其中实数a,b是常数.查看答案和解析>>
科目:高中数学 来源:2011年广东省深圳市高考数学一模试卷(文科)(解析版) 题型:解答题
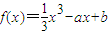 ,其中实数a,b是常数.
,其中实数a,b是常数.查看答案和解析>>
科目:高中数学 来源:2010年重庆市高考数学试卷(理科)(解析版) 题型:解答题
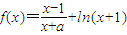 ,其中实数a≠1.
,其中实数a≠1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com