
【题目】解关于x的不等式ax2﹣(a+1)x+1<0.
【答案】解:当a=0时,不等式的解为{x|x>1};
当a≠0时,分解因式a(x﹣ ![]() )(x﹣1)<0
)(x﹣1)<0
当a<0时,原不等式整理得:x2﹣ ![]() x+
x+ ![]() >0,即(x﹣
>0,即(x﹣ ![]() )(x﹣1)>0,
)(x﹣1)>0,
不等式的解为{x|x>1或x< ![]() };
};
当0<a<1时,1< ![]() ,不等式的解为{x|1<x<
,不等式的解为{x|1<x< ![]() };
};
当a>1时, ![]() <1,不等式的解为{x|
<1,不等式的解为{x| ![]() <x<1};
<x<1};
当a=1时,不等式的解为.
【解析】当a=0时,得到一个一元一次不等式,求出不等式的解集即为原不等式的解集;当a≠0时,把原不等式的左边分解因式,然后分4种情况考虑:a小于0,a大于0小于1,a大于1和a等于1时,分别利用求不等式解集的方法求出原不等式的解集即可.
【考点精析】掌握解一元二次不等式是解答本题的根本,需要知道求一元二次不等式![]()
![]() 解集的步骤:一化:化二次项前的系数为正数;二判:判断对应方程的根;三求:求对应方程的根;四画:画出对应函数的图象;五解集:根据图象写出不等式的解集;规律:当二次项系数为正时,小于取中间,大于取两边.
解集的步骤:一化:化二次项前的系数为正数;二判:判断对应方程的根;三求:求对应方程的根;四画:画出对应函数的图象;五解集:根据图象写出不等式的解集;规律:当二次项系数为正时,小于取中间,大于取两边.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥ABCD﹣PGFE中,底面ABCD是直角梯形,侧棱垂直于底面,AB∥DC,∠ABC=45°,DC=1,AB=2,PA=1.
(Ⅰ)求PD与BC所成角的大小;
(Ⅱ)求证:BC⊥平面PAC;
(Ⅲ)求二面角A﹣PC﹣D的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
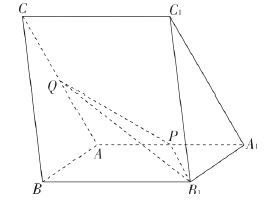
【题目】如图,三棱柱![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 分别为棱
分别为棱![]() 的中点.
的中点.
(1)在平面![]() 内过点
内过点![]() 作
作![]() 平面
平面![]() 交
交![]() 于点
于点![]() ,并写出作图步骤,但不要求证明.
,并写出作图步骤,但不要求证明.
(2)若侧面![]() 侧面
侧面![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中,真命题是( )
A.?x0∈R,![]()
B.?x∈R,![]()
C.“a>1,b>1”是“ab>1”的充要条件
D.设![]() ,
, ![]() 为向量,则“|
为向量,则“|![]() ?
?![]() |=|
|=|![]() ||
||![]() |”是“
|”是“![]() ∥
∥![]() ”的充要条件
”的充要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层.某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元.该建筑物每年的能源消耗费用C(单位:万元)与隔热层厚度x(单位:cm)满足关系:C(x)= ![]() (0≤x≤10),若不建隔热层,每年能源消耗费用为8万元.设f(x)为隔热层建造费用与20年的能源消耗费用之和.
(0≤x≤10),若不建隔热层,每年能源消耗费用为8万元.设f(x)为隔热层建造费用与20年的能源消耗费用之和.
(1)求k的值及f(x)的表达式.
(2)隔热层修建多厚时,总费用f(x)达到最小,并求最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在边长为2的正方体ABCD﹣A1B1C1D1中,E是BC的中点,F是DD1的中点,
(1)求点A到平面A1DE的距离;
(2)求证:CF∥平面A1DE;
(3)求二面角E﹣A1D﹣A的平面角大小的余弦值.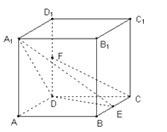
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在R上的偶函数,且x≤0时,f(x)=log ![]() (﹣x+1).
(﹣x+1).
(1)求f(x)的解析式;
(2)若f(a﹣1)<﹣1,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com