Question

已知，a 、b Î (0，p )，求2a －b 的值．

Answer 1

答案：略
解析：

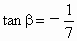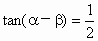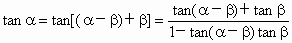
解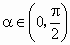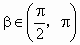：∵，， ∴ ， ∵，∴，， ∴a －b Î (－p ，0) 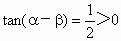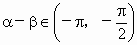∵，∴， 2a －b =a ＋(a －b )Î (－p ，0)． 而tan(2a －b )=1，∴． 已知a －b 及b 角的正切，显然要求2a －b 的正切，该题必须通过角变换，2a －b =a ＋(a －b )，a =(a －b )＋b ，故需先求出a 角的正切．

提示：

该小题的解题思路是利用角变换求出了2a －b 角的正切值，难点和关键是通过判断值的大小缩小2a －b 角的范围．若仅仅根据已知条件告诉的a 和b 的范围判断2a －b 的范围，这个范围是非常大的，这个范围是(－p ，p )则正切值为1的角有和，导致错误答案．