
【题目】已知椭圆![]() 经过点
经过点![]() ,
, ![]() 的四个顶点构成的四边形面积为
的四个顶点构成的四边形面积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)在椭圆![]() 上是否存在相异两点
上是否存在相异两点![]() ,使其满足:①直线
,使其满足:①直线![]() 与直线
与直线![]() 的斜率互为相反数;②线段
的斜率互为相反数;②线段![]() 的中点在
的中点在![]() 轴上,若存在,求出
轴上,若存在,求出![]() 的平分线与椭圆相交所得弦的弦长;若不存在,请说明理由.
的平分线与椭圆相交所得弦的弦长;若不存在,请说明理由.
科目:高中数学 来源: 题型:
【题目】近年来城市“共享单车”的投放在我国各地迅猛发展,“共享单车”为人们出行提供了很大的便利,但也给城市的管理带来了一些困难,现某城市为了解人们对“共享单车”投放的认可度,对![]() 年龄段的人群随机抽取
年龄段的人群随机抽取![]() 人进行了一次“你是否赞成投放共享单车”的问卷调查,根据调查结果得到如下统计表和各年龄段人数频率分布直方图:
人进行了一次“你是否赞成投放共享单车”的问卷调查,根据调查结果得到如下统计表和各年龄段人数频率分布直方图:
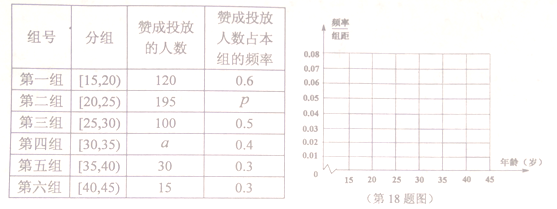
(1)补全频率分布直方图,并求![]() 的值;
的值;
(2)在第四、五、六组“赞成投放共享单车”的人中,用分层抽样的方法抽取7人参加“共享单车”骑车体验活动,求第四、五、六组应分别抽取的人数;
(3)在(2)中抽取的7人中随机选派2人作为正副队长,求所选派的2人没有第四组人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() ,函数 f(x)=x2(x-a) ,若f'(1)=1 .
,函数 f(x)=x2(x-a) ,若f'(1)=1 .
(1)求 a 的值并求曲线 y=f(x) 在点(1,f(1)) 处的切线方程y=g(x) ;
(2)设h(x)=f'(x)+g(x) ,求 h(x) 在 [0,1] 上的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,两个椭圆![]() ,
, ![]() 内部重叠区域的边界记为曲线C,P是曲线C上的任意一点,给出下列四个判断:
内部重叠区域的边界记为曲线C,P是曲线C上的任意一点,给出下列四个判断:
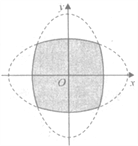
①P到F1(-4,0)、F2(4,0)、E1(0,-4)、E2(0,4)四点的距离之和为定值;
②曲线C关于直线y=x、y=-x均对称;③曲线C所围区域面积必小于36.
④曲线C总长度不大于6π.上述判断中正确命题的序号为________________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2﹣6x﹣4y+4=0,点P(6,0).
(1)求过点P且与圆C相切的直线方程l;
(2)若圆M与圆C外切,且与x轴切于点P,求圆M的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com