
【题目】已知椭圆![]() ,过
,过![]() 上一点
上一点![]() 的切线
的切线![]() 的方程为
的方程为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设过点![]() 且斜率不为
且斜率不为![]() 的直线交椭圆于
的直线交椭圆于![]() 两点,试问
两点,试问![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得 ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
【答案】(Ⅰ)![]() (Ⅱ)存在点
(Ⅱ)存在点![]() 使得
使得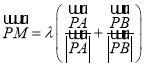 .
.
【解析】试题分析: (I)由直线与椭圆相切,联立方程,有且只有两个相同的实数根,求出![]() 之间的一个关系式,再根据点
之间的一个关系式,再根据点![]() 在椭圆上,求出
在椭圆上,求出![]() 的值,得出椭圆方程;(II)联立直线AB的方程与椭圆方程,求出两根之和,两根之积的表达式,由已知得出PM平分
的值,得出椭圆方程;(II)联立直线AB的方程与椭圆方程,求出两根之和,两根之积的表达式,由已知得出PM平分![]() ,得出直线PA与PB倾斜角互补,它们的斜率和为零,求出
,得出直线PA与PB倾斜角互补,它们的斜率和为零,求出![]() 的值.
的值.
试题解析:(Ⅰ)由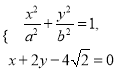 消去
消去![]() 并整理得
并整理得
![]() .
.
∵椭圆![]() 与直线
与直线![]() 相切,
相切,
∴![]() ,
,
化简得![]() ,①
,①
又点![]() 在椭圆
在椭圆![]() 上,∴
上,∴![]() .②
.②
由①②得![]() ,
, ![]() .
.
∴椭圆![]() 的方程为
的方程为![]() .
.
(Ⅱ)存在.理由如下:
设直线![]() 的方程为
的方程为![]() ,
,
联立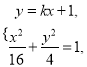 消去
消去![]() 并整理得
并整理得![]() .
.
![]() .
.
设![]() ,
, ![]() ,则
,则![]() ,
, ![]() .
.
假设存在点![]() 满足条件,
满足条件,
由于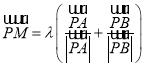 ,所以
,所以![]() 平分
平分![]() .
.
易知直线![]() 与直线
与直线![]() 的倾斜角互补,∴
的倾斜角互补,∴![]() ,
,
即![]() ,即
,即![]() .(
.(![]() )
)
将![]() ,
, ![]() 代入(
代入(![]() )并整理得
)并整理得
![]() ,
,
∴![]() ,
,
整理得![]() ,即
,即![]() ,
,
∴当![]() 时,无论
时,无论![]() 取何值均成立.
取何值均成立.
∴存在点![]() 使得
使得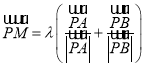 .
.
点睛: 本题主要考查了求椭圆方程等相关知识,属于中档题. 本题路: (I)由直线与椭圆相切,联立直线与椭圆方程,消去![]() ,得到一个关于
,得到一个关于![]() 的一元二次方程,判别式为零,得到
的一元二次方程,判别式为零,得到![]() 之间的一个关系式, 再根据点
之间的一个关系式, 再根据点![]() 在椭圆上,求出
在椭圆上,求出![]() 的值,得出椭圆方程;(II)设直线AB的方程为
的值,得出椭圆方程;(II)设直线AB的方程为![]() ,联立直线与椭圆方程, 消去
,联立直线与椭圆方程, 消去![]() ,得到一个关于
,得到一个关于![]() 的一元二次方程,求出两根之和,两根之积的表达式,由向量之间的关系得出PM平分
的一元二次方程,求出两根之和,两根之积的表达式,由向量之间的关系得出PM平分![]() ,所以
,所以![]() , 求出
, 求出![]() 的值.
的值.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:
【题目】已知定义在(﹣∞,0)∪(0,+∞)上的奇函数f(x)满足f(2)=0,且在(﹣∞,0)上是增函数;又定义行列式![]() =a1a4﹣a2a3; 函数g(θ)=
=a1a4﹣a2a3; 函数g(θ)=![]() (其中0≤θ≤
(其中0≤θ≤![]() ).
).
(1)证明:函数f(x)在(0,+∞)上也是增函数;
(2)若函数g(θ)的最大值为4,求m的值;
(3)若记集合M={m|任意的0≤θ≤![]() , g(θ)>0},N={m|任意的0≤θ≤
, g(θ)>0},N={m|任意的0≤θ≤![]() , f[g(θ)]<0},求M∩N.
, f[g(θ)]<0},求M∩N.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,点P到两点(0,﹣![]() ),(0,
),(0,![]() )的距离之和等于4,设点P的轨迹为C,直线y=kx+1与C交于A,B两点.
)的距离之和等于4,设点P的轨迹为C,直线y=kx+1与C交于A,B两点.
(1)写出C的方程;
(2)若![]() ⊥
⊥![]() , 求k的值.
, 求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A={x| ![]() <3x<9},B={x|log2x>0}.
<3x<9},B={x|log2x>0}.
(1)求A∩B和A∪B;
(2)定义A﹣B={x|x∈A且xB},求A﹣B和B﹣A.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x),当x,y∈R时,恒有f(x+y)=f(x)+f(y).当x>0时,f(x)>0
(1)求证:f(x)是奇函数;
(2)若f(1)= ![]() ,试求f(x)在区间[﹣2,6]上的最值.
,试求f(x)在区间[﹣2,6]上的最值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数, ![]() ).以原点
).以原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,与直角坐标系
轴正半轴为极轴,与直角坐标系![]() 取相同的长度单位,建立极坐标系.设曲线
取相同的长度单位,建立极坐标系.设曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)设![]() 为曲线
为曲线![]() 上任意一点,求
上任意一点,求![]() 的取值范围;
的取值范围;
(Ⅱ)若直线![]() 与曲线
与曲线![]() 交于两点
交于两点![]() ,
, ![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com