
【题目】已知函数![]() .
.
(1)当![]() 时,证明:
时,证明: ![]() ;
;
(2)当![]() 时,函数
时,函数![]() 单调递增,求
单调递增,求![]() 的取值范围.
的取值范围.
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:(1)![]() 时,
时, ![]() 即证
即证![]() ,只需证明
,只需证明![]() ,利用导数研究函数
,利用导数研究函数![]() 的单调性,根据单调性可得
的单调性,根据单调性可得![]() ,从而可得原不等式成立;(2) 依题
,从而可得原不等式成立;(2) 依题![]() 在
在![]() 上恒成立,讨论三种情况:①当
上恒成立,讨论三种情况:①当![]() 时,
时, ![]() 单调递增;
单调递增; ![]() ,符合题意;②当
,符合题意;②当![]() 时,
时, ![]() ,不符合题意,舍去;③当
,不符合题意,舍去;③当![]() 存在部分
存在部分![]() 不合题意,综合三种情况可得结果.
不合题意,综合三种情况可得结果.
试题解析:证明:(1)当![]() 时,即证:
时,即证: ![]() ,
,
![]() ,令
,令![]() ,
,
则![]() ,当
,当![]() 时,有
时,有![]() .
.
当![]() 时,
时, ![]() 单调递增;
单调递增;
当![]() 时,有
时,有![]() .当
.当![]() 时,
时, ![]() 单调递减,
单调递减, ![]() .
.![]() 取等号条件不致,
取等号条件不致,
![]() (此问可以参考如图理解).
(此问可以参考如图理解). ![]() .
.
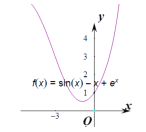
(2)依题![]() 在
在![]() 上恒成立,
上恒成立,
令![]() ,
,
又令![]() ,所以当
,所以当![]() 时,
时, ![]() 在
在![]() 上单调递增,
上单调递增,
![]() ,因此
,因此![]() ,
,
![]() ,讨论:
,讨论:
①当![]() 时,
时, ![]() 单调递增;
单调递增; ![]() ,符合题意
,符合题意
②当![]() 时,
时, ![]() ,不符合题意,舍去.
,不符合题意,舍去.
③当![]() .
.
![]() ,当
,当![]() 时,
时, ![]() 在
在![]() 时单调递减,
时单调递减,
当![]() 时,
时, ![]() 在
在![]() 单调递减,
单调递减, ![]() ,不符合题意舍去.
,不符合题意舍去.
综上: ![]() .
.


科目:高中数学 来源: 题型:
【题目】给定下列四个命题,其中真命题是( )
A.垂直于同一直线的两条直线相互平行
B.若一个平面内的两条直线与另一个平面都平行,那么这两个平面相互平行
C.垂直于同一平面的两个平面相互平行
D.若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】判断下列命题的真假并说明理由.
(1)某个整数不是偶数,则这个数不能被4整除;
(2)若![]() ,且
,且![]() ,则
,则![]() ,且
,且![]() ;
;
(3)合数一定是偶数;
(4)若![]() ,则
,则![]() ;
;
(5)两个三角形两边一对角对应相等,则这两个三角形全等;
(6)若实系数一元二次方程![]() 满足
满足![]() ,那么这个方程有两个不相等的实根;
,那么这个方程有两个不相等的实根;
(7)若集合![]() ,
,![]() ,
,![]() 满足
满足![]() ,则
,则![]() ;
;
(8)已知集合![]() ,
,![]() ,
,![]() ,如果
,如果![]() ,那么
,那么![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设x=1与x=2是函数f(x)=aln x+bx2+x的两个极值点.
(1)试确定常数a和b的值;
(2)判断x=1,x=2是函数f(x)的极大值点还是极小值点,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某钢管生产车间生产一批钢管,质检员从中抽出若干根对其直径(单位: ![]() )进行测量,得出这批钢管的直径
)进行测量,得出这批钢管的直径![]() 服从正态分布
服从正态分布![]() .
.
(1)当质检员随机抽检时,测得一根钢管的直径为![]() ,他立即要求停止生产,检查设备,请你根据所学知识,判断该质检员的决定是否有道理,并说明判断的依据;
,他立即要求停止生产,检查设备,请你根据所学知识,判断该质检员的决定是否有道理,并说明判断的依据;
(2)如果钢管的直径![]() 满足
满足![]() 为合格品(合格品的概率精确到0.01),现要从60根该种钢管中任意挑选3根,求次品数
为合格品(合格品的概率精确到0.01),现要从60根该种钢管中任意挑选3根,求次品数![]() 的分布列和数学期望.
的分布列和数学期望.
(参考数据:若![]() ,则
,则![]() ;
; ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】分层抽样是将总体分成互不交叉的层,然后按照一定的比例,从各层独立地抽取一定数量的个体,组成一个样本的抽样方法;在《九章算术》第三章“衰分”中有如下问题:“今有甲持钱五百六十,乙持钱三百五十,丙持钱一百八十,凡三人俱出关,关税百钱.欲以钱多少衰出之,问各几何?”其译文为:今有甲持560钱,乙持350钱,丙持180钱,甲、乙、丙三人一起出关,关税共100钱,要按照各人带钱多少的比例进行交税,问三人各应付多少税?则下列说法错误的是( )
A. 甲应付![]() 钱 B. 乙应付
钱 B. 乙应付![]() 钱
钱
C. 丙应付![]() 钱 D. 三者中甲付的钱最多,丙付的钱最少
钱 D. 三者中甲付的钱最多,丙付的钱最少
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年2月25日第23届冬季奥运会在韩国平昌闭幕,中国以1金6银2铜的成绩结束本次冬奥会的征程.某校体育爱好者协会在高三年级某班进行了“本届冬奥会中国队表现”的满意度调查(结果只有“满意”和“不满意”两种),按分层抽样从被调查的学生中随机抽取了11人,具体的调查结果如下表:
某班 | 满意 | 不满意 |
男生 | 2 | 3 |
女生 | 4 | 2 |
(Ⅰ)若该班女生人数比男生人数多4人,求该班男生人数和女生人数
(Ⅱ)在该班全体学生中随机抽取一名学生,由以上统计数据估计该生持满意态度的概率;
(Ⅲ)若从该班调查对象中随机选取2人进行追踪调查,记选中的2人中对“本届冬奥会中国队表现”满意的人数为![]() ,求随机变量
,求随机变量![]() 的分布列及其数学期望.
的分布列及其数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com